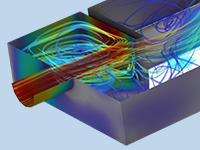
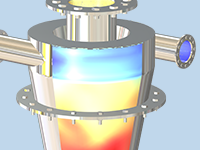
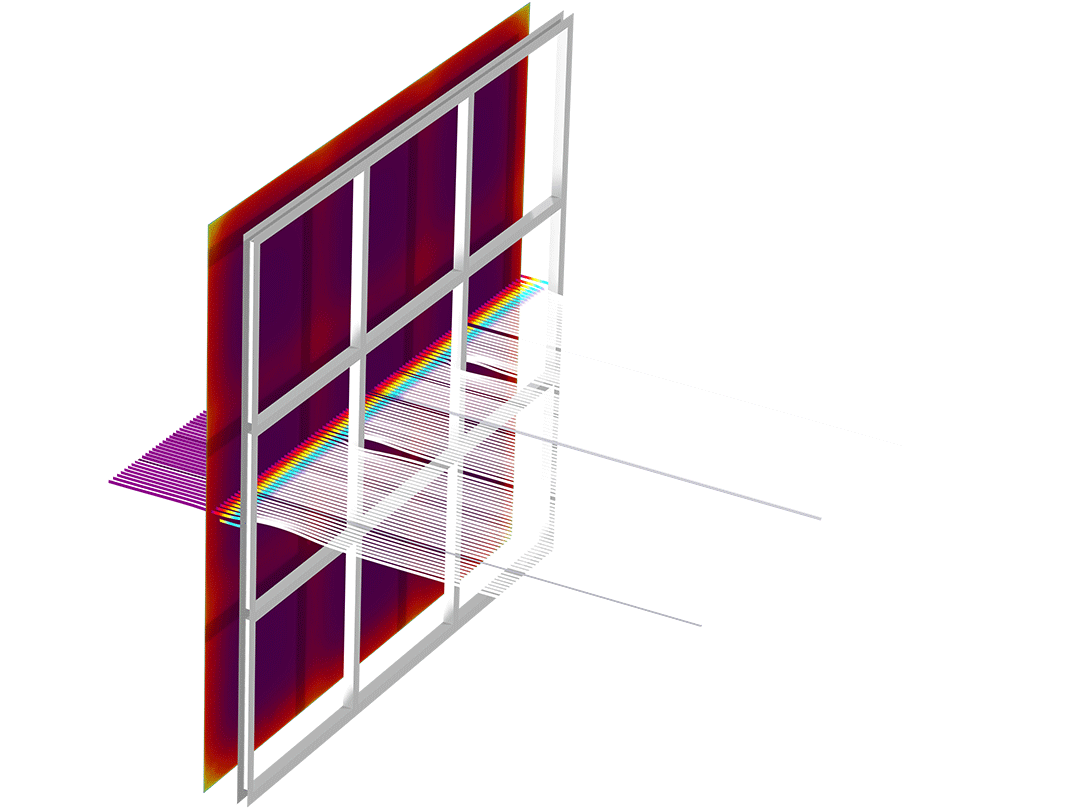
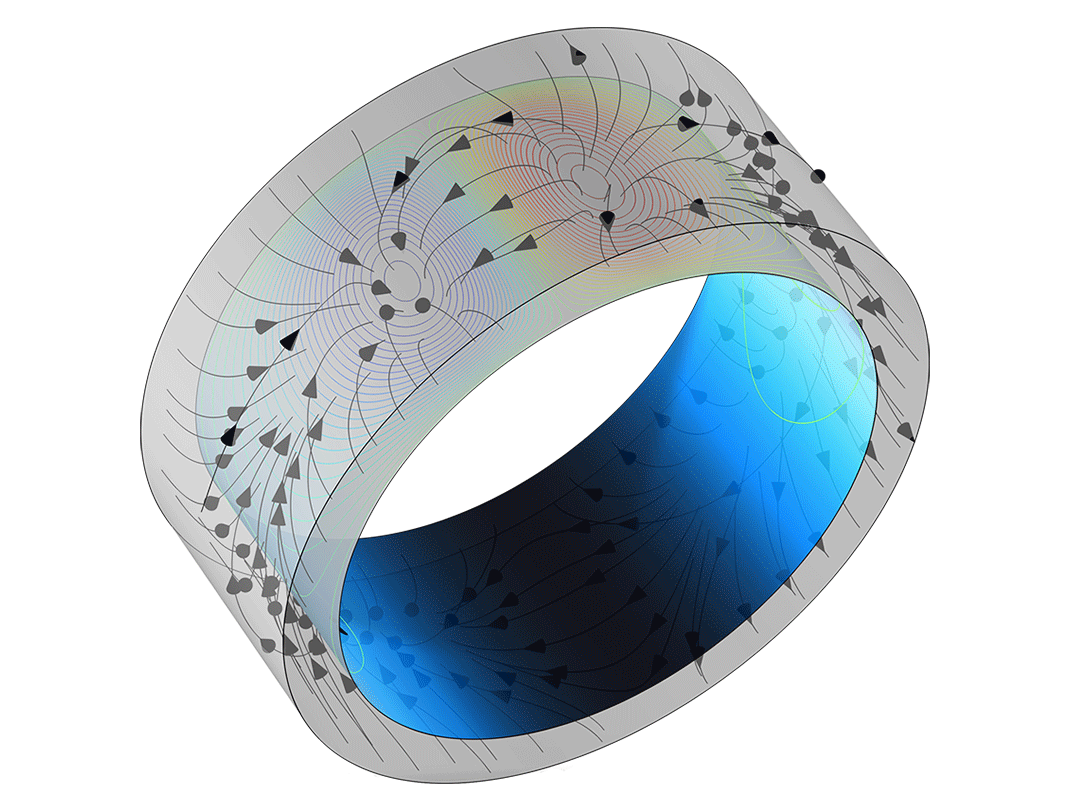
Laminar and Creeping Flow
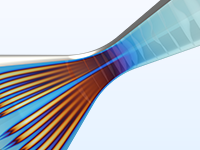
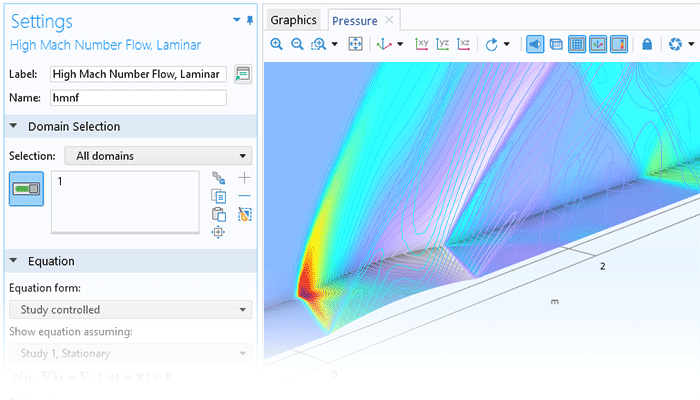
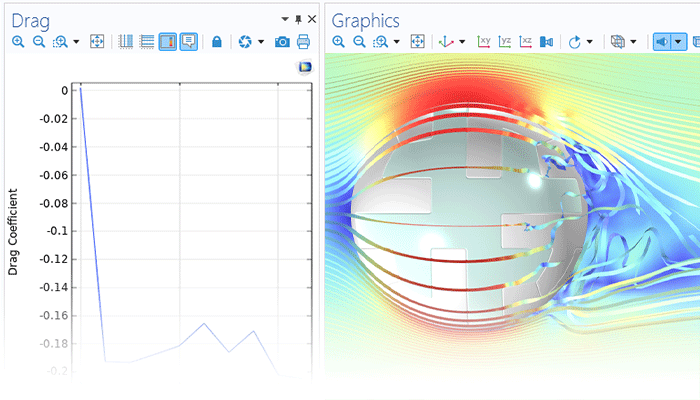
Model transient and steady laminar flow with the Navier–Stokes equations or creeping flow with the Stokes equations.
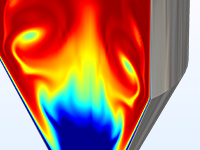
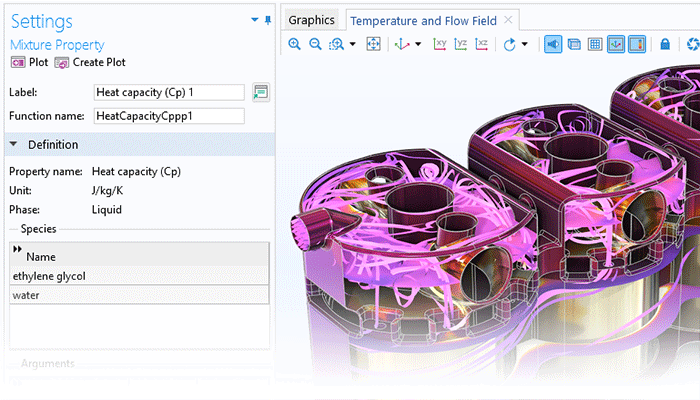
In addition to modeling fluids with constant density and viscosity, you can study fluids where the viscosity and density depend on the temperature, local composition, electric field, or any other modeled field or variable. In general, density, viscosity, and momentum sources can be arbitrary functions of any dependent variable, as well as derivatives of dependent variables.
For non-Newtonian fluids, you can use the generic yet predefined rheology models for viscosity, such as Power Law, Carreau, Bingham, Herschel–Bulkley or Casson for easy model setup.
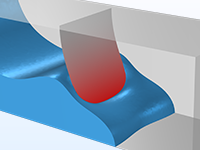
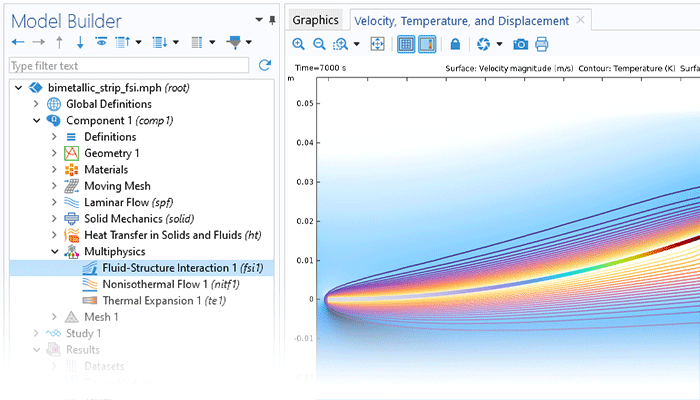
You can also model laminar flow in moving structures, for example opening and closing valves or rotating impellers.