Nonlinear Structural Materials for Multiphysics Modeling
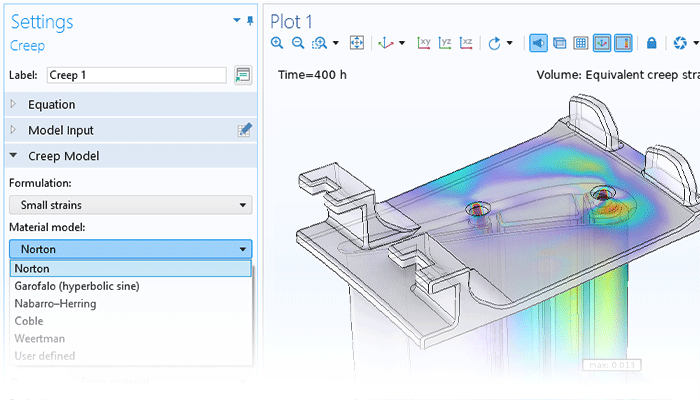
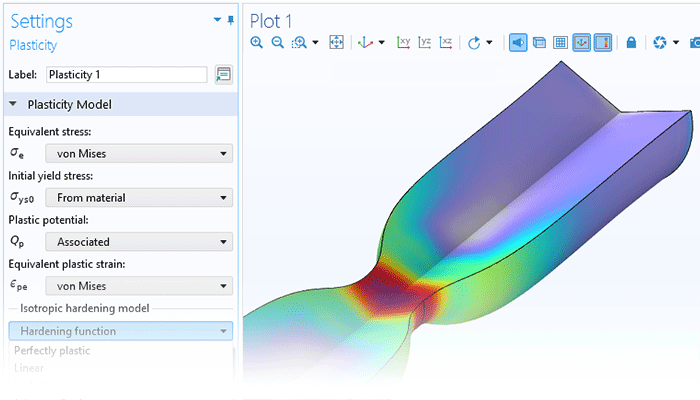
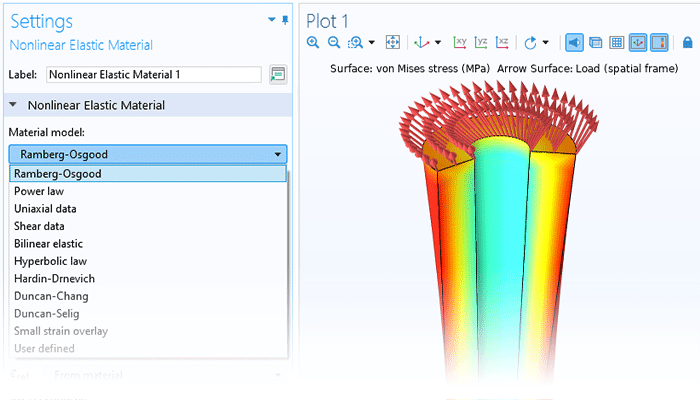
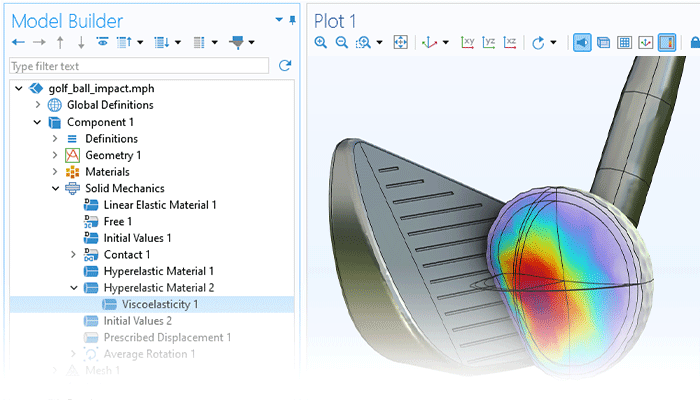
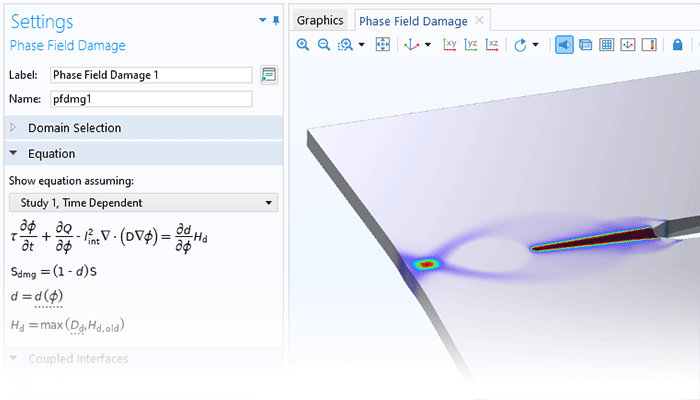
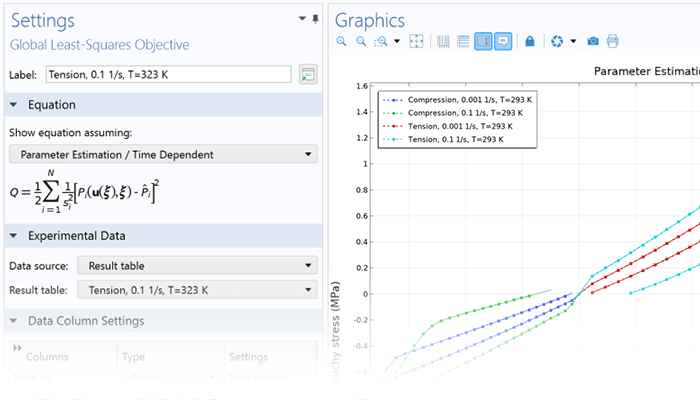
The functionality for modeling nonlinear materials augments all of the structural analyses available within the Structural Mechanics Module or the MEMS Module. Combine linear elastic, hyperelastic, or nonlinear elastic materials with nonlinear effects such as plasticity, creep, viscoplasticity, or damage, and use the versatility of the COMSOL Multiphysics® simulation software to include multiphysics couplings with a couple of clicks. You can even define your own models based on, for example, stress or strain invariants. Create your own flow rules and creep laws, as well as your own strain energy density functions for hyperelasticity.
Multiphysics capabilities are built into the COMSOL Multiphysics® software platform for modeling thermal expansion, pore pressure, fluid–structure interaction, and many more multiphysics phenomena. All of the structural materials included in the Nonlinear Materials Module are multiphysics capable.