
During his life, John Scott Russell chased his passion for science — literally. While watching horses pull a boat through a shallow canal, he noticed a wave behaving strangely and followed it for one or two miles on horseback. For the rest of his life, he continued to chase this wave (which he called the “wave of translation”) figuratively, persevering even when his theories were ridiculed by scientists. Did Scott Russell ever catch up to his wave?
A Horse, a Flyboat, and a Curious Naval Architect
If you lived in Glasgow in the 1830s, one of the best ways to get around Scotland was a horse-drawn flyboat on the Glasgow, Paisley and Ardrossan Canal. Flyboats were lightweight, long, and narrow. They were pulled through the shallow water of the canal by horses.


A modern view of Glasgow, Scotland, (left) and a canal in central Scotland, home of the rotating boat lift known as the Falkirk Wheel (right).
One day, William Houston, an owner of one of the flyboat companies, was traveling down a canal when the horse pulling his flyboat was startled and bolted. Houston noticed something strange: The water exhibited no resistance. The ship glided fast (similar to what we now call “hydroplaning”), and the turbulence from the boat’s movement didn’t damage the shores of the canal. (Ref. 1)
Enter John Scott Russell, a naval architect from Glasgow. When he heard about the phenomenon Houston observed, he thought that witnessing it for himself could give him insight into boat design. While observing the canal, one of the horses suddenly stopped. A wave formed under the middle of the boat, moved to the prow, and then took off past the boat entirely. Scott Russell followed the wave, first on foot and then on his horse. He was astounded to see that the wave kept going at the same size and pace. He later called it “the wave of translation” and described the event as “the happiest day of my life.” (Ref. 2)

John Scott Russell in 1847. Image in the public domain in the United States, via Wikimedia Commons.
Scott Russell devoted two years to replicating the wave of translation so he could study it further. He even built a 30-foot basin to test his different theories. Eventually, he observed some unique properties of these waves, which he now called solitary waves. According to Scott Russell, a solitary wave:
- Travels over large distances in a stable manner
- Travels at a speed that is dependent on its size
- Has a width that is dependent on the water’s depth
- Does not combine with other waves (instead, large ones overtake smaller ones)
- Splits into two waves of different sizes if it is too large for the depth of the water
Animation showing the behavior of a solitary wave.
He also categorized these waves into four types:
- Waves of translation, which involve mass transfer and are either solitary or followed by a series of secondary waves
- Oscillatory waves, groups of successive waves (such as the waves created by wind)
- Capillary waves, which are caused by a very small agitation of the water and depend on surface tension
- Corpuscular waves, rapid successions of solitary waves (such as sound waves)
Scott Russell presented his findings at a British Science Association meeting in Edinburgh, describing the waves and the mechanics behind them. His work contained a few misinterpretations of the foundations of mechanical laws — understandably so, as his background was in architecture, not physics. Scientists at the time balked at his theories and distrusted his lack of engineering and physics expertise.
And so began a lifetime — actually, many lifetimes — of investigating the behavior of solitary waves.
Initial Reactions to the Solitary Wave
At first, Scott Russell didn’t earn many fans in the scientific community regarding his theory of solitary waves. George Biddell Airy, who studied the behavior of waves in relation to the tides, did not hold Scott Russell in high regard and believed that solitary waves contradicted Pierre-Simon Laplace’s theory of fluid mechanics. Laplace’s equations, as we know, are integral to the study of fluid dynamics today. (Ref. 1)
George Gabriel Stokes, of the famed Navier-Stokes equations, also did not support the possibility of solitary waves and initially condemned their relation to tides and sound. Over time, as he researched finite oscillatory waves, he changed his stance and admitted that a theoretical solitary wave was plausible. (Ref. 1)
Meanwhile: A Return to Shipbuilding
Scott Russell never gave up the subject of solitary waves, but he continued what his main job description entailed: building ships. He used his research into waves to design a special ship prow, which was based on the shape of a versed sine wave, that could better handle water resistance.
In the 1850s, Isambard Kingdom Brunel asked for Scott Russell’s help regarding a steamship called the Great Eastern. Brunel had designed the ship, which was slated to be the largest ship of its time (he affectionately called it his “Great Babe”). The ship could purportedly travel from England to Australia without needing to refuel.

The Great Eastern before its first launch. Image in the public domain in the United States, via Wikimedia Commons.
Scott Russell was successful in taking Brunel’s designs and building the Great Eastern, which eventually made many transatlantic voyages. However, his success was tarnished when Brunel passed away shortly before launch and a major accident occurred during the ship’s maiden voyage. Around this time, Scott Russell was also having trouble with his finances and was dealing with the seizure of his assets.
How the Tides Turned: Boussinesq and the KdV Equation
Toward the end of his life, Scott Russell’s solitary wave was still rebuked by scientists, and he was bankrupt. Fortunately, things were about to change.
Joseph Valentin Boussinesq, a protégé of Adhémar Jean Claude Barré de Saint-Venant known for his contributions to the field of fluid dynamics, did not write off Scott Russell like others at the time. Instead, he subjected every aspect of waves and tides to mathematical analysis. In 1872, Boussinesq attempted to explain shallow water waves, which led to an equation that proved solitary waves are theoretically possible. He even mentioned Scott Russell in his paper on the subject in 1877. Lord Rayleigh independently developed similar theories on waves and also supported Scott Russell. (Ref. 1)
Finally, two scientists had spoken out in support of his work! Then, in 1882, Scott Russell passed away at the age of 74 on the Isle of Wight, England. But the story doesn’t end there.
In 1895, Diederik Korteweg and Gustav de Vries expanded on Boussinesq’s work and developed an equation that proves solitary waves are theoretically possible. The KdV equation doesn’t introduce dissipation, which means it can be used to describe waves that travel long distances while retaining their shape and speed. The equation is also simpler than Boussinesq’s version and gives a better solution. (Ref. 2) Because of these advantages, the KdV equation is still used to understand wave behavior — in its many forms — today.
Modern Research into Solitons
Research into solitary waves picked up in 1965, when researchers Martin Krustal and Norman Zabusky studied the KdV equation in more detail. They found that solitary waves can occur not just theoretically but also naturally, coining the term solitons to describe them. In addition, solitons were not just thought of in the context of water waves anymore — with research into applications for optics, acoustics, and other areas.
Krustal, along with researchers Gardner, Greene, and Miura, developed the inverse scattering transform in 1967. This method can be used to find the exact solution of the KdV equation and also demonstrates the elastic collisions between waves, originally observed by Krustal and Zabusky. (Ref. 2)

A hydrodynamic soliton. Image by Christophe.Finot et Kamal HAMMANI. Licensed under CC BY-SA 2.5, via Wikimedia Commons.
Moving forward, scientists Zakharov and Shabat used a formulation developed by Peter Lax to solve the nonlinear Schrödinger equation, which describes the evolution of the slowly varying envelope of a general wave packet. Ablowitz, Kaup, Newell, and Segur later came up with a more systematic approach to solving the nonlinear Schrödinger equation, which is now known as the AKNS method. (Ref. 2)
All of this mathematical activity around solitons caught the attention of the scientific community in a way that Scott Russell couldn’t. Over the next 30 years, solitons in a wide range of different fields were researched, including geomechanics, oceanography, astrophysics, quantum mechanics, and more.
Solitons for Fiber Optics
Optical fibers are an important and practical application area for solitons. The linear dispersion properties of a fiber level out a soliton, while its nonlinear properties help the soliton achieve a focusing effect. The result is a very stable pulse that can travel for what seems like forever.
The behavior was first observed by a group at Bell Labs led by Linn Mollenauer in the 1980s that aimed to apply solitons to long-distance telecommunication systems. In the 1990s, a team of MIT researchers added optical filters to a transmission system in an attempt to maximize an optical soliton’s propagation distance. Using this method, Mollenauer’s group sent a 10-Gbit/s signal more than 20,000 km — impressive for the time. (Ref. 2) During the 2000s, optical soliton research ventured into the field of vector solitons, which have two distinct polarization components.
Current research from Lahav et al. aims to create solitons that are stable in all three dimensions, known as “light bullets”. This requires the simultaneous cancellation of diffraction and dispersion, which has been achieved with a highly structured material, but not with an unstructured one that can be used in practical applications. The Lahav group has investigated the fundamental properties of 3D solitons to develop more technological applications of solitons for fiber optics. They have also developed a method that involves shining a repetitive string of light pulses into a special material called “strontium barium niobate” to create a self-guided beam and cancel out the dispersion. This method creates a string of 3D solitons that could potentially be used in advanced nonlinear optics and optical information processing. (Ref. 3)
Equation-Based Modeling Enables Out-of-the-Box Soliton Analysis
The solution to the KdV equation tells us that the speed of a soliton determines its amplitude and width. By investigating this effect, we can better predict the behavior and limitations of solitons for optical applications. Simulation can be used to visualize soliton behavior beyond numerical equations, without setting up resource-intensive or costly optical experiments. Besides demonstrating how speed influences the amplitude and width of a wave, simulation also shows how solitons collide and reappear while maintaining their shape (like the solitary waves Scott Russell observed “overtaking” each other in the ocean).
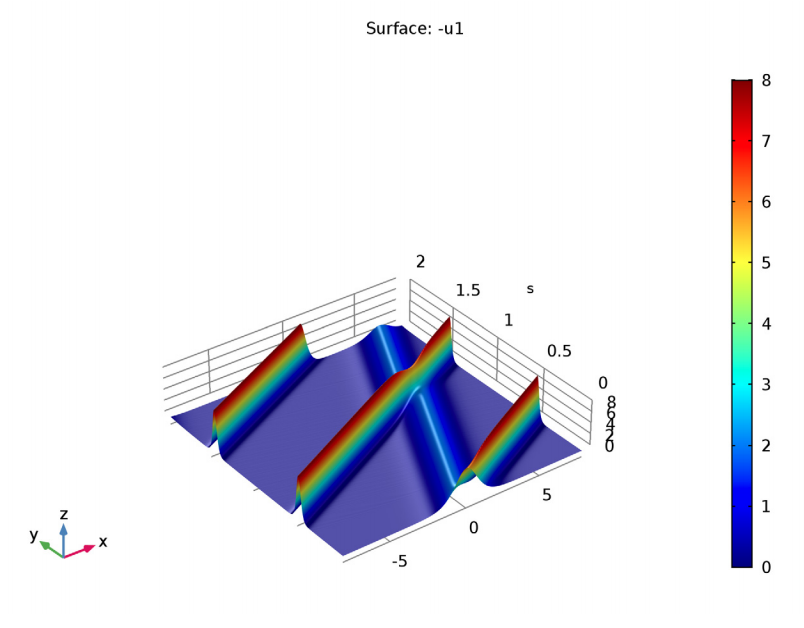
Simulation results that show solitons colliding and reappearing. Image from The KdV Equation and Solitons tutorial model.
Predefined physics settings are an efficient and easy option for straightforward modeling tasks; however, optical solitons are anything but. Equation-based modeling enables you to expand what is normally possible with simulation for problems that require flexibility and creativity. Using equation-based modeling, you can seamlessly implement the KdV equation into the COMSOL Multiphysics® software by adding partial differential equations (PDEs) and ordinary differential equations (ODEs). You can even create a physics interface from your custom settings so that you don’t have to start from scratch the next time you need to set up a model.
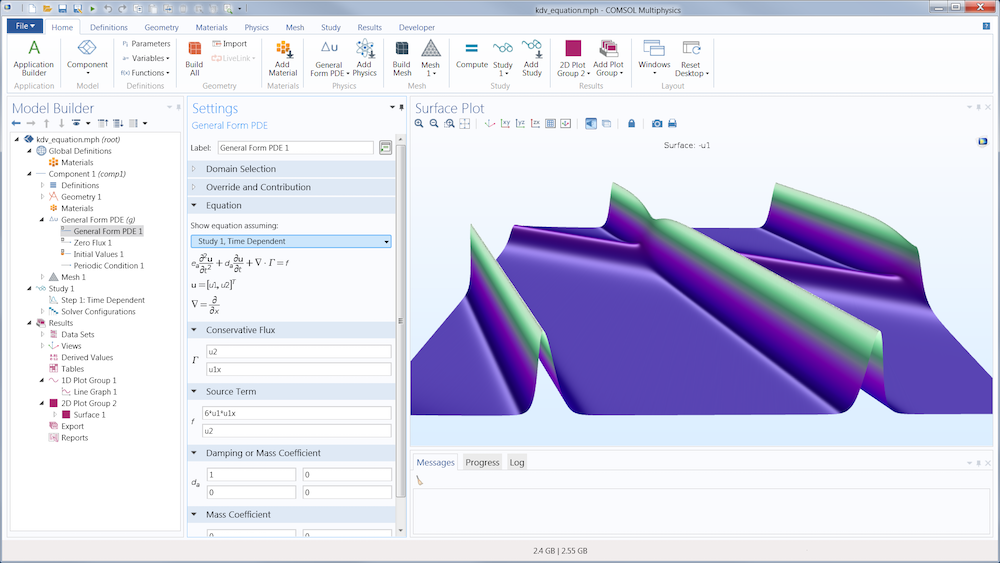
Adding a PDE to a soliton model in the COMSOL Multiphysics graphical user interface (GUI), an example of equation-based modeling.
Equation-based modeling functionality makes it possible to simulate an initial pulse in an optical fiber as well as the resulting waves or solitons.
Concluding Thoughts on John Scott Russell, the Individual Wave
In 1885, Scott Russell’s book The Wave of Translation in the Oceans of Water, Air and Ether was published posthumously. It included his speculations on the physics of matter and how we can find the depths of the atmosphere and universe by computing the velocity of sound and light, respectively. (Ref. 4) Even at the end of his life, Scott Russell continued to theorize on how we can apply mathematics to the observable world as well as the significance of solitons in modern physics. If only he could have seen the development of the KdV equation or recent advancements in optics.
One of Scott Russell’s supporters, Osborne Reynolds, made a fitting observation in his own research of solitary waves: In deep water, groups of waves travel faster than the individual waves from which they were made. (Ref. 1) Perhaps we can think of John Scott Russell as the individual wave, inspiring others to keep moving toward a common goal.
Next Step
Learn more about equation-based modeling, and the other features and functionality in COMSOL Multiphysics, by clicking the button below.
References
- O. Darrigol, “The Spirited Horse, the Engineer, and the Mathematician: Water Waves in Nineteenth-Century Hydrodynamics,” Archive for History of Exact Sciences, vol. 58, pp. 21–95, 2003.
- B. Kath and B. Kath, “Making Waves: Solitons and Their Optical Applications,” SIAM News, vol. 31, no. 2, pp. 1–5, 1998.
- F.W. Wise, “Solitons divide and conquer,” Nature, vol. 554, pp. 179–180, 2018.
- Topics in Current Physics: Solitons, R.K. Bullough and P.J. Caudrey, eds., Springer-Verlag, pp. 373–379, 1980.





Comments (0)