
In the previous part of our Electromagnetic Device series, we showed you how to model a linear electromagnetic plunger attached to a spring and damper and compute the position, velocity, and electromagnetic forces. Here, we will demonstrate an actuator that includes a blocker/stopper to restrict linear motion. We will also discuss how to model the contact and release of this actuator using the Events, Magnetic Fields, Moving Mesh, and Global ODEs and DAEs interfaces.
Modeling a Linear Electromagnetic Actuator with a Blocker
Today, we will modify the Electromagnetic Plunger tutorial model discussed in a previous blog post by adding a blocker with a matching shape that restricts the linear motion of the plunger. The remaining components of the plunger device include:
- Multi-turn coil
- Magnetic core
- Nonmagnetic guider
- Magnetic plunger
We divide the air region between the plunger and the blocker, as shown in the image below and to the right, to make it compatible for the structure (mapped mesh) for linear oscillation. The damper and spring are attached to one end of the plunger.
When the transient current passes through the solenoid’s coil, it causes the creation of a magnetic field in the plunger and magnetic core. The resulting magnetic field produces an attraction force between these two parts. The plunger then accelerates, moving in an upward motion against the attached spring to be in contact with the blocker. The plunger will remain in contact as long as the electromagnetic force is larger than the restoring force due to the spring. The velocity of the plunger will become zero as soon as it is in contact with the blocker. However, when the coil is turned off, the force from the spring is larger and the plunger goes back to its original position. We will model this contact and release mechanism through the Events interface using this example. You can download the model file and associated slides here.
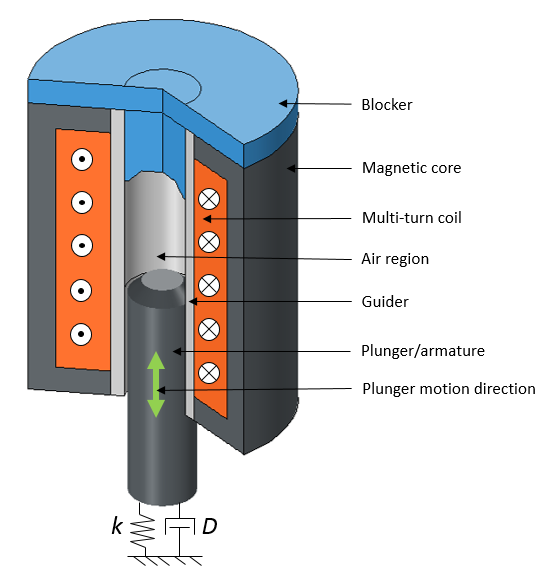
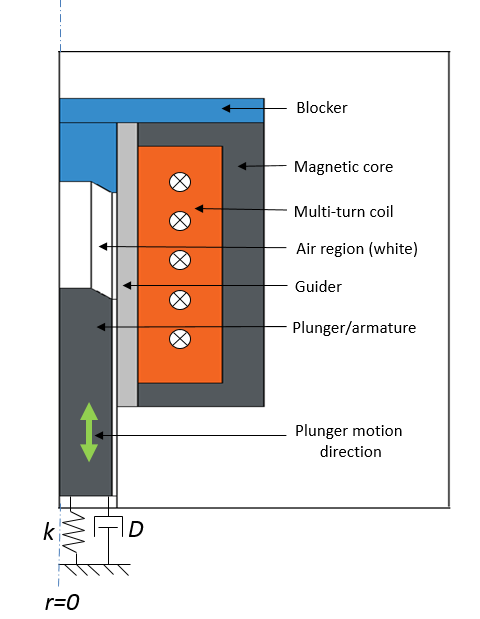
An electromagnetic plunger with a blocker in both 3D (left) and 2D axisymmetric views (right).
Solving for the Electromagnetic Fields
In our plunger model, we simulate the electromagnetic fields in the device using the Magnetic Fields interface. We add an Ampère’s Law node for modeling the magnetic components (plunger and magnetic core) using the constitutive relation set to an H-B curve. We compute the electromagnetic force in the plunger using the Maxwell’s stress tensor method by adding a Force Calculation node. With the help of the Multi-Turn Coil feature, we model the solenoidal winding and pass a transient current using the rectangular function.
Simulating Linear Motion
To model the plunger’s linear motion, we add the Moving Mesh interface to only the moving domains (the plunger and air domains on the left of the identity pair). This is the same approach used in these oscillating magnet and electromagnetic plunger examples. However, the moving mesh setup in this particular example is a bit complicated. This is because the mesh between the plunger and the blocker is contracted to almost zero volume. A volumetric mesh of zero is numerically impossible to model; therefore, we fixed the height of this contracted mesh to a finite value (0.5 mm in this case) to represent the contact between the plunger and the blocker.
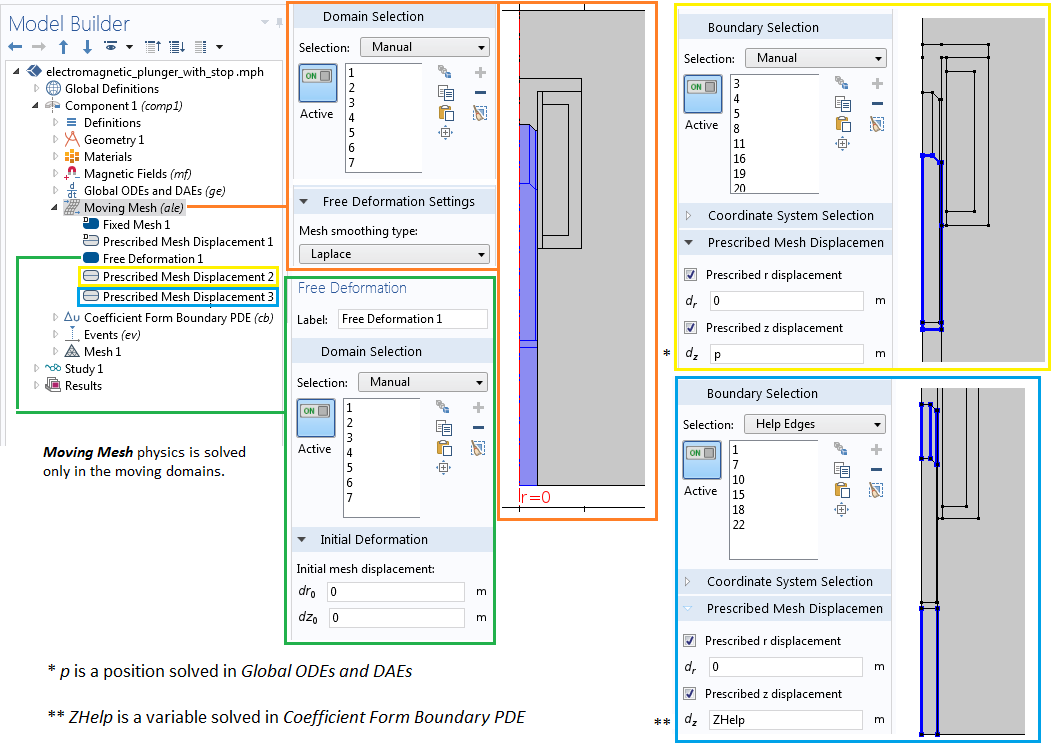
The Moving Mesh interface settings, depicting the variable coupling from the Coefficient Form Boundary PDE and Global ODEs and DAEs interfaces.
In the settings shown above, you will notice that the plunger and a small portion of the air domain are assigned a prescribed displacement of the position variable, p, in the z direction and no displacement in the r direction. However, on the side boundaries (Help Edges) of the contracting or expanding air region, the prescribed displacement in the z direction is assigned a new variable, ZHelp. This variable is solved using a separate Coefficient Form Boundary PDE interface, as shown in the following image. For more information about this functionality, refer to these previous blog posts on using the deformed mesh interfaces for modeling translational motion and modeling rotations and linear translations.
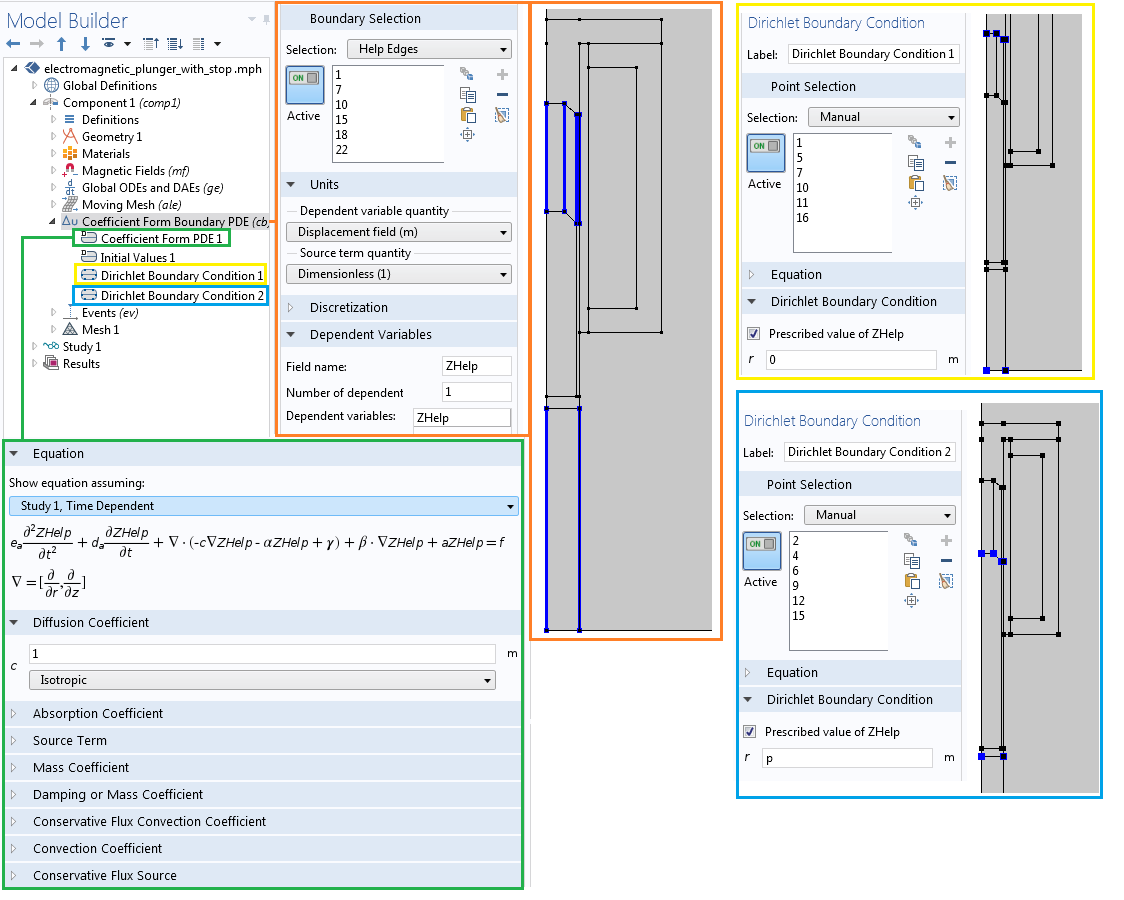
The Coefficient Form Boundary PDE interface setup for solving the ZHelp variable.
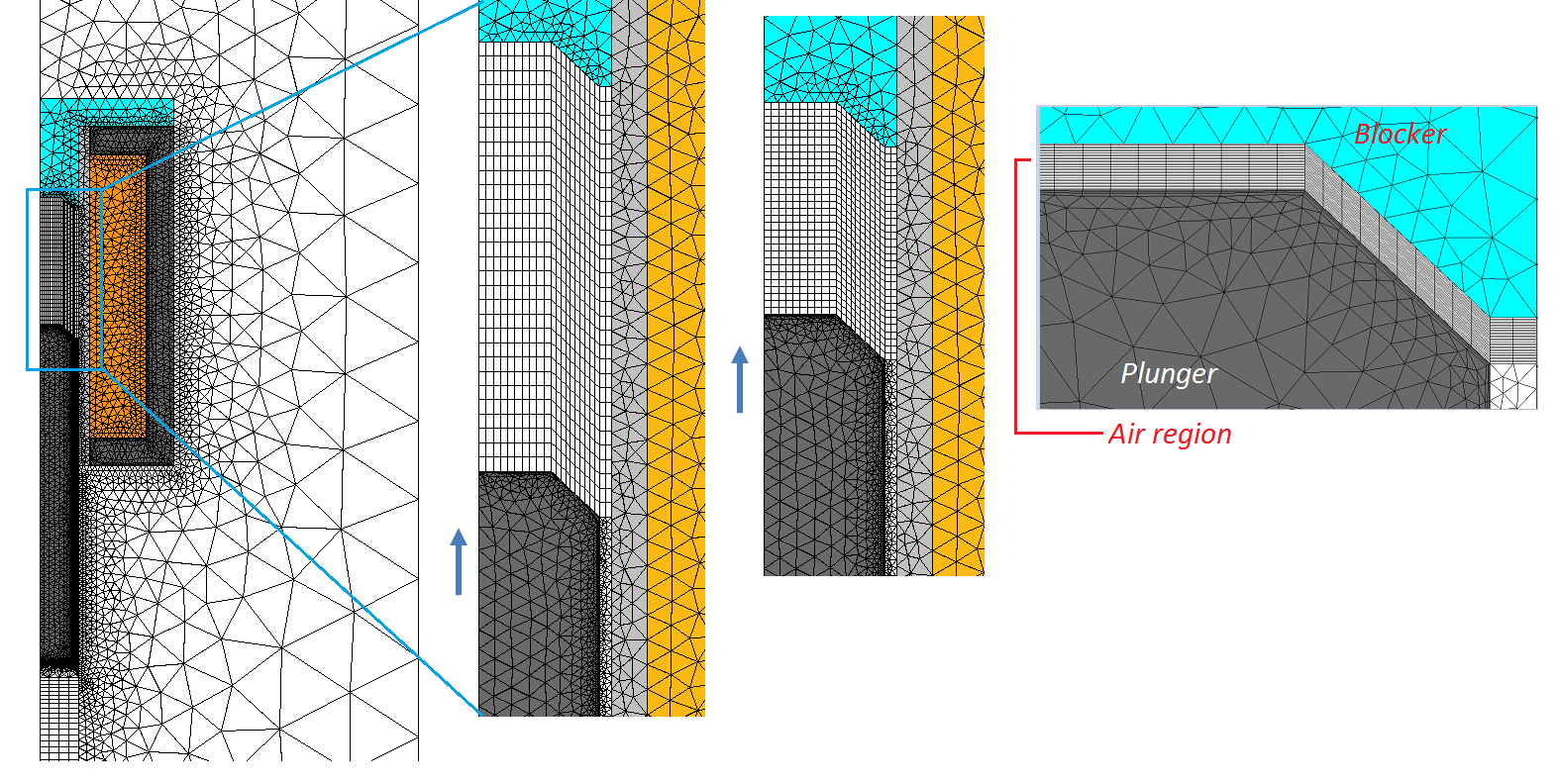
The mesh images of the plunger, illustrating the contraction of the structured mesh in the air region.
Modeling Contact and Release Operation Using the Events Interface
In the next step, we’ll add the Events interface to model the instance when the plunger is in contact with the stopper/blocker or is released when the coil is turned off. The Events interface, which is available within the Mathematics > ODE and DAE interfaces branch, can be added like any other physics interface within COMSOL Multiphysics.
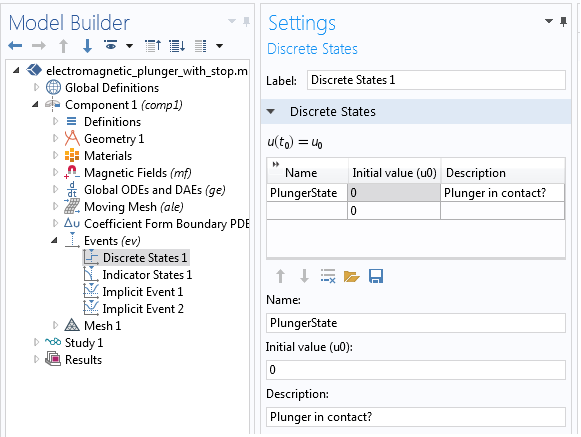
Let’s first use the Events interface to define a pair of discrete variables that are discontinuous in time and ideal for modeling the in-contact or off-contact conditions for the plunger. As shown in the image below, the discrete variable, PlungerState, is defined with an initial value of zero; i.e., the plunger is not in contact using the Discrete State feature. The initial value of zero indicates that the plunger is not in contact when the simulation begins. The PlungerState variable is used in the Global ODEs and DAEs interface to appropriately model the plunger in contact or off contact. The variable can have two discrete values, zero or one, depending on the value condition satisfied by the indicator states. This setting is similar to the control logic in a thermostat discussed by my colleague Water Frei in a previous blog post.
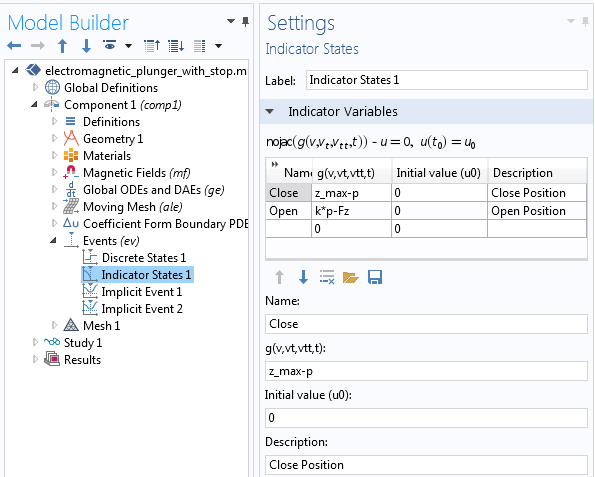
The Discrete States interface is used to define the state of the plunger, which is initially not in contact (left). Two indicator states in the Events interface depend on the position and the forces (right).
Next, we need to define the indicator states, indicating the condition to trigger the value of PlungerState from 0 to 1 or vice versa. The objective of the indicator states is to define variables that will indicate when an event will occur. Two indicator states are defined: Close and Open. The Close indicator variable is defined as: z_max-p, which changes smoothly from positive to negative, as the position is above the parameter z_max. Here, z_max is the position at which the plunger will be in contact with the stopper/blocker. Similarly, the Open indicator variable is defined as k*p-Fz and changes smoothly from negative to positive when the force due to the attached spring, k*p, is larger than the electromagnetic force, F_z, on the plunger.
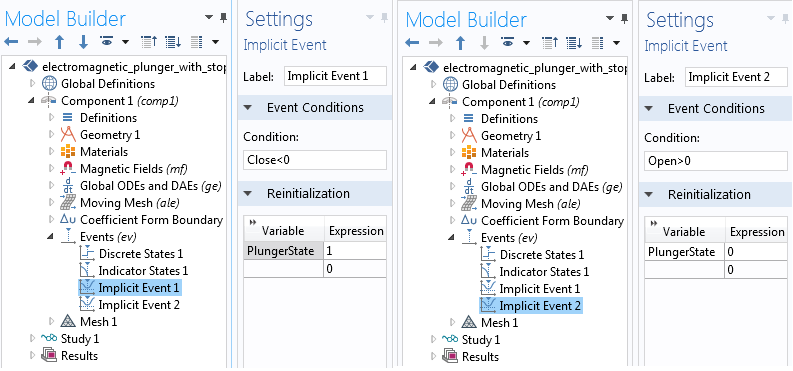
The settings for the implicit events within the Events interface in which the PlungerState variable is reinitialized.
Since we do not know the exact time when these events will trigger, we will use the appropriate logical conditions to change the state of the plunger using the Implicit Events feature. As shown in the above image, we will add two Implicit Events features to reinitialize the state of the plunger to be either zero or one, based on whether the Open and Close indicator states are greater or less than zero, respectively. During the transient simulation, these events will trigger if the logical condition is fulfilled. When the event is triggered, the transient solver will stop and restart with the newly initialized PlungerState variable in the position and the velocity equations in the Global ODEs and DAEs interface, as discussed in the following section.
Modeling the Dynamics of the Plunger Device
The previous blog post in this series goes into detail about how to implement the global equations into the Global ODEs and DAEs interface, which account for the motion of the electromagnetic plunger attached to the spring using a variety of variables, including:
- Spring constant
- Damping coefficient
- Plunger position
- Velocity
- Plunger mass
- Electromagnetic force of the plunger against the spring
Concerning the PlungerState indicator, when the PlungerState variable is one (in contact), the equation for the velocity given by (2) is reset to v=0, and the equation for the position given by (3) is p-z_{max}=0. However, if the plunger is not in contact, the equations for velocity and positions are given by (2) and (3), respectively.

The implementation of differential equations for the velocity and position using the Global ODEs and DAEs interface and logical expression, which implement the contact and release operation of the plunger with the help of the PlungerState variable.
Analyzing the Findings
The representative results obtained from the time-domain simulation of the plunger model are highlighted below. The results show the instance when the plunger is in contact with the blocker and released when the current in the coil is turned off.
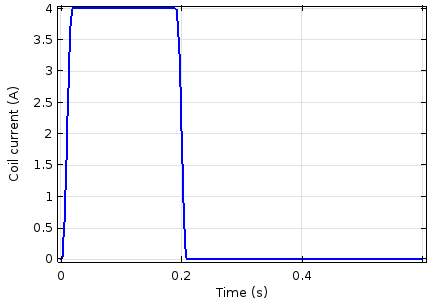
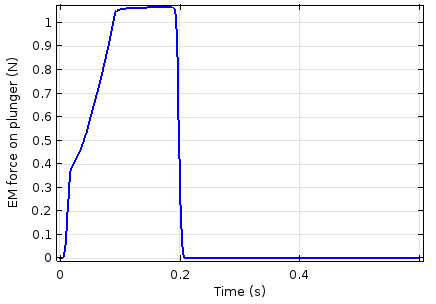
The current through the coil (left) and electromagnetic force (right) as a function of time.
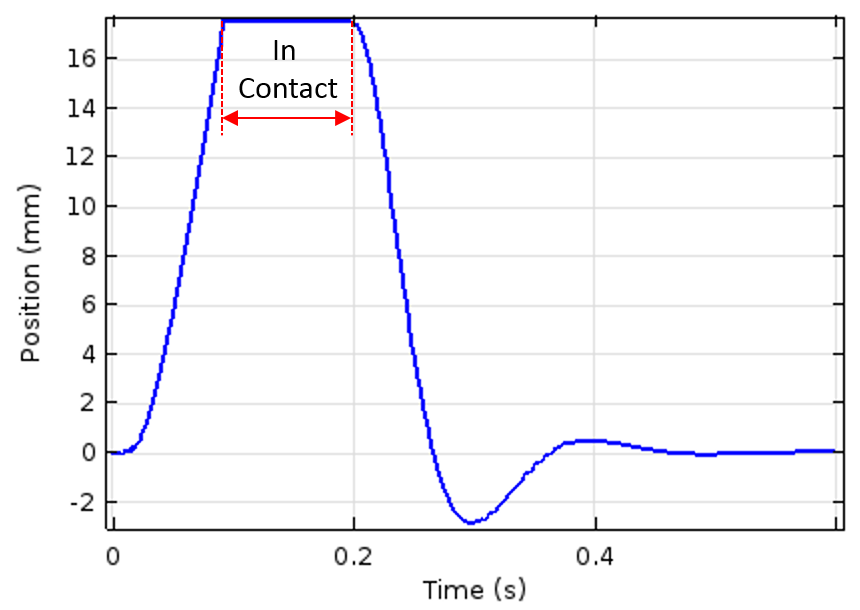
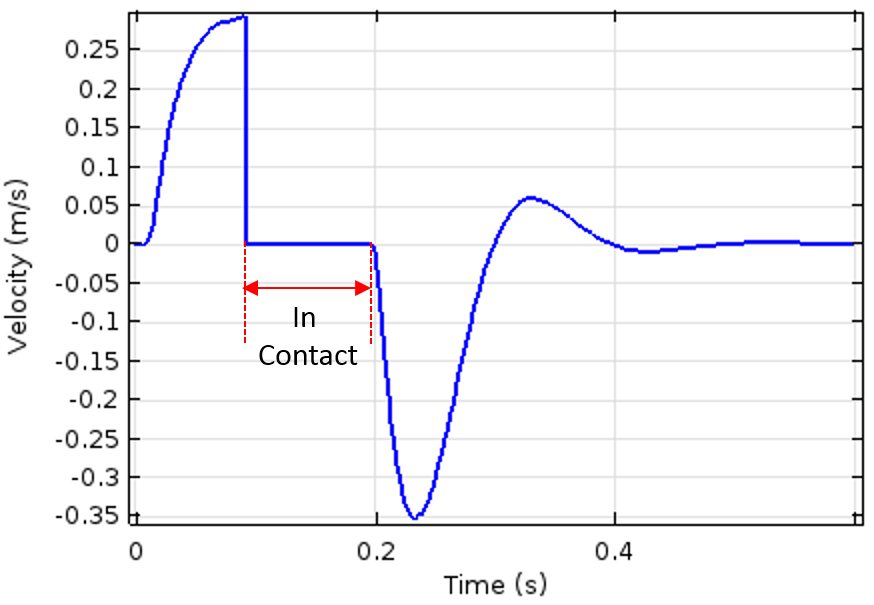
The plunger position (left) and velocity (right) as a function of time. The time interval at which the plunger remains in contact with the blocker is also indicated in the plot.
A 3D animation of the magnetic flux density norm plot for the plunger with the included blocker (left) and a graph plotting the device’s corresponding position and velocity, as well as the current moving through the coil.
Summary
Here, we extend the modeling technique of an electromagnetic plunger outlined in a previous blog post by introducing the Events interface to model the contact and release operation of the plunger. We calculate the transient electromagnetic force in the plunger using Magnetic Fields physics and evaluate the linear/translational motion in the plunger by coupling it with the Moving Mesh and Coefficient Form Boundary PDE interfaces. We also compute the transient position and velocity of the plunger using the Global ODEs and DAEs interface by coupling it with all of the other interfaces.
Learn More About Modeling Other Electromagnetic Devices
- Try it yourself: Download the Electromagnetic Plunger with Stopper tutorial model from the Application Gallery
- Take a step back and explore the tutorial model of an electromagnetic plunger without a stopper
- Check out the other blog posts included in our Electromagnetic Device series





Comments (3)
amir rezvanian
November 22, 2018hello
you defined the force calculation to recognize and calculate the magnetic force in specific area. if we want to recognize the magnetic flux density in specific area and use that to solve ODE. how we can do that?
best regards
Brianne Costa
November 27, 2018Hello Amir,
Thank you for your comment.
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
James Grosssnickle
April 3, 2020Hello,
How do I create that animation in COMSOL? a 3D cut with graphs in the same graphic is exactly what i need to generate.
thank you