Blog Posts Tagged Technical Content
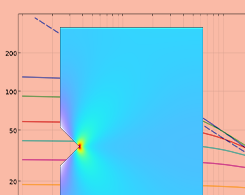
How Should I Evaluate Singular Stress Fields?
Explore the properties of singular stress fields and see some possible approaches for evaluating them in COMSOL Multiphysics®.
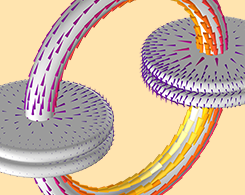
Learning from the Two-Capacitor Paradox: Do Capacitance and Inductance Exist?
What is the two-capacitor paradox? How can it be resolved with modeling and simulation? Do capacitance and inductance exist? Get answers here.

Introduction to the Composite Materials Module
Explore the Composite Materials Module, an add-on to COMSOL Multiphysics® that includes specialized functionality for modeling layered composite structures.
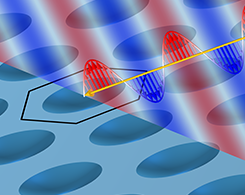
Understanding Higher-Order Diffraction
Explore how to use the Ewald sphere to study diffraction from planar periodic structures. (Interact directly with the model to get the full picture!)

The Power of the Batch Sweep
Have you ever run a large parametric sweep on your workstation overnight, only to discover the next morning that the parametric solver is still not finished? Enter the batch sweep.
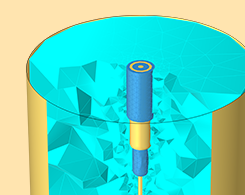
Understanding the Excitation Options for Modeling Electric Currents
Learn about the capabilities of COMSOL Multiphysics® for modeling frequency-domain electric currents in this in-depth guide.
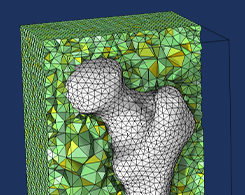
Generating a Simulation Mesh of a Femur From 3D Data
You can create a simulation mesh from 3D data in COMSOL Multiphysics®. This capability comes in handy when modeling irregular shapes.
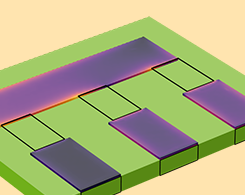
Combining Volumetric Conductor Models and Lumped Elements
With the AC/DC Module, it is possible to connect a full-fidelity volumetric conductor model to a lumped circuit element model. Learn how here.
