
When developing systems that involve fluid–structure interaction (FSI), such as bridges, aircraft, and biomedical applications, engineers may want to use topology optimization early on in the design process. However, many topology optimization methods are only available for FSI problems within an academic scope. Researchers developed a new methodology to help alleviate this issue…
FSI and Topology Optimization
Fluid–Structure Interaction
Fluid–structure interaction (FSI) is a multiphysics coupling between the laws that describe fluid dynamics and structural mechanics. When designing a variety of systems — such as automobiles, aircraft, and spacecraft — accounting for FSI is crucial. If these effects are ignored, it can lead to catastrophe.

The Tacoma Narrows Bridge collapsing in 1940. Image in the public domain in the United States, via Wikimedia Commons.
In November 1940, tragedy struck Tacoma, Washington, when the original Tacoma Narrows Bridge collapsed just four months after its opening. At the time of its destruction, it was the third-longest suspension bridge in the world, connecting Tacoma and the Kitsap Peninsula.
Originally, many believed the bridge collapsed due to resonance, but we have since learned it was a result of aeroelastic flutter. This large-scale structural design failure demonstrated the importance of studying FSI, especially when designing long-span bridges. (The Tacoma Narrows Bridge has since been rebuilt into a pair of twin suspension bridges).
FSI also plays an important role in modeling blood flow. For example, biomedical engineers can simulate FSI to accurately predict the behavior of human heart valves and address various cardiac health issues.
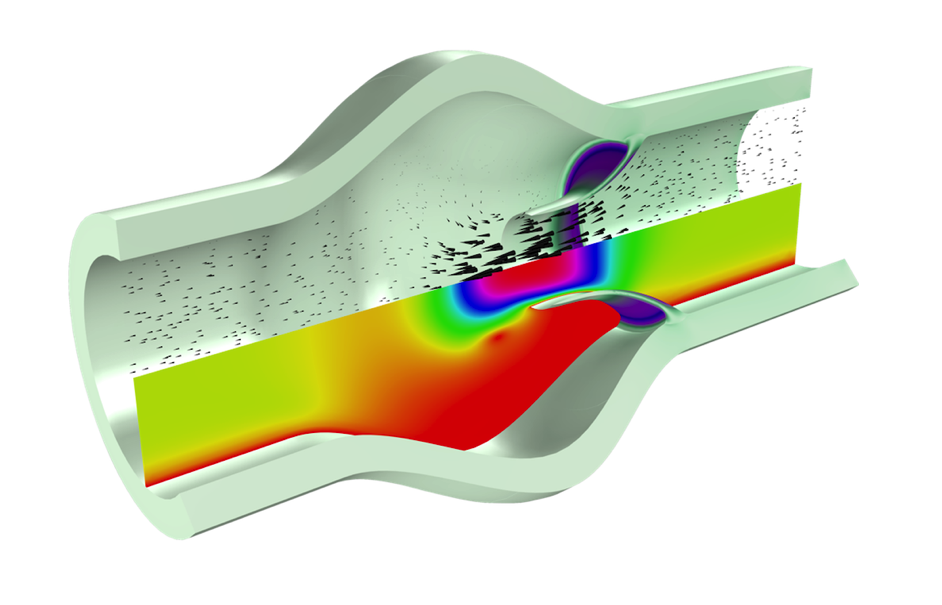
An FSI model of a heart valve opening, showing velocity magnitude and the surface structural stress. Red denotes low velocities (behind the valve downstream) and high velocities (in the center orifice) and purple represents high stress values.
Topology Optimization
Topology optimization is one of the three main categories of optimization (the other two being parametric and shape optimization).
Topology optimization is a very powerful tool, as it helps us generate new topologies for an engineering structure given an objective function and set of constraints. However, its uses are typically limited to single-physic designs (Ref. 1).
Keeping this problem in mind, researchers from the University of São Paulo and the University of California San Diego set out to develop a new methodology for applying a topology optimization method to structures under design-dependent FSI loads.
Integrating a New Topology Optimization Method into LiveLink™ for MATLAB®
At the University of São Paulo (USP), researchers are working to advance the sustainable use of natural gas. As the nature of much of their work deals with FSI problems, the Multiphysics Systems Optimization Laboratory (MSOL) at USP developed a new methodology for integrating a topology optimization method, Topology Optimization of Binary Structures (TOBS), into an FEA package, the COMSOL Multiphysics® software, via the LiveLink™ for MATLAB® interfacing product.
The TOBS method (Ref. 2) was recently and independently developed by Renato Picelli (formerly a postdoctoral associate at Cardiff University, UK) and Raghavendra Sivapuram (University of California San Diego). This method uses sequential approximate problems; sensitivity filtering; integer linear programming; and binary design variables, which is helpful when working with design-dependent physics interactions. The MSOL group at USP developed a framework based on geometry trimming (GT), creating the TOBS-GT method for fluid-structure design. (Learn more about the implementation of this methodology in Ref. 1.)
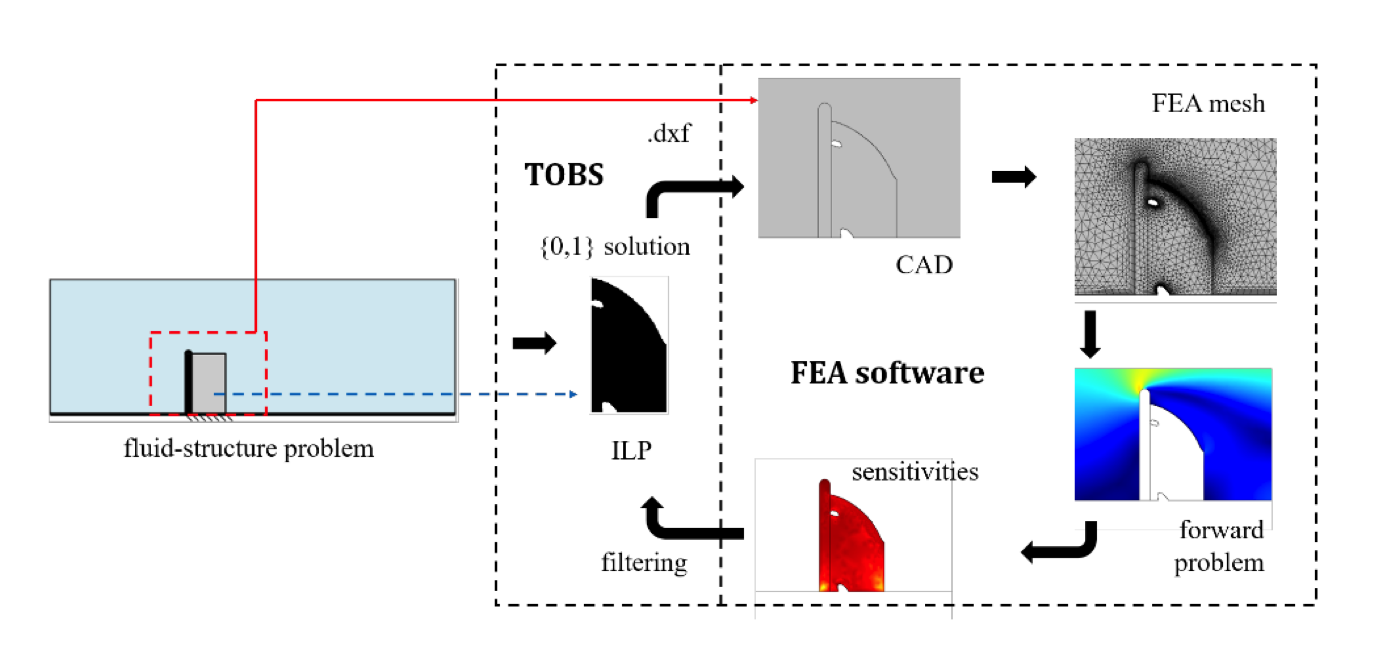
A diagram showcasing the TOBS-GT algorithm for fluid-structure design.
Shahin Ranjbarzadeh, a postdoctoral associate at the University of São Paulo and member of the MSOL group at USP said: “In the beginning, the TOBS method was just applied to the topology optimization of a structure. By developing the TOBS-GT, we applied the idea to fluid–structure interaction problems involving laminar, turbulent, and non-Newtonian flow.” This work represents the first attempt to consider integer linear programming in FSI problems.
The main benefit of joining the TOBS method with LiveLink™ for MATLAB® is that there is no grayscale in the results, because the TOBS method is based on binary design variables (0,1). “Because the TOBS method is based on zero and one, we don’t have any intermediate value in the topology optimization results,” says Ranjbarzadeh. Furthermore, with TOBS-GT we can adapt the mesh according to the physics requirements.
To highlight the features of the proposed method, the researchers shared examples of its use in a 2020 paper published in Springer Nature, their first published work showcasing the method.
Pneumatic Devices
“When we wrote the first paper, we were looking for a real application to include,” said Ranjbarzadeh. Ultimately, the researchers opted to showcase the capabilities of the method for lessening the compliance of linear elastic systems under FSI loads, all subject to volume constraints. All of the examples showed smoothly converged results.
Several of the examples from the research paper are based on pneumatic devices.
“I think this method will help a lot to predict the failure in pneumatic devices, such as in compressors or applications with rotation,” said Ranjbarzadeh.
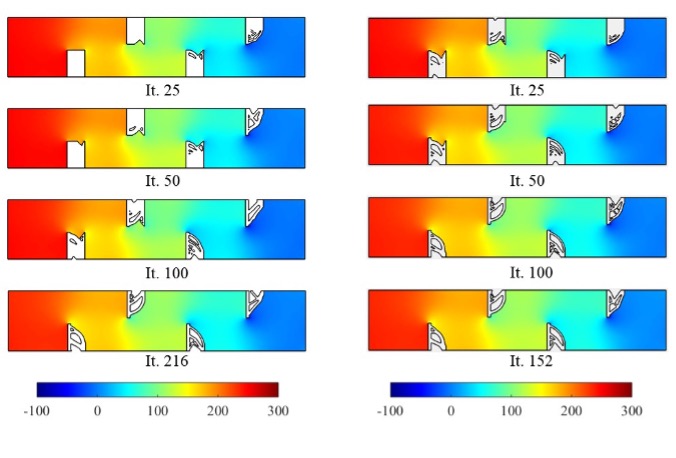
FSI topology optimization solution for minimum structural compliance, subject to a single global volume constraint (left). Seal topology optimization solution for minimum structural compliance, subject to four separate volume constraints, one per wall (right). Both colorized plots highlight the fluid pressure field (in Pa).
3D FSI Topology Optimization
In addition to results demonstrated in the published paper, a 3D example of FSI topology optimization was also carried out.
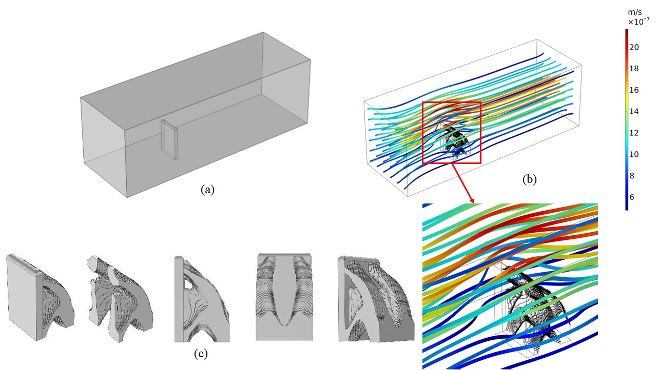
3D FSI topology optimization domain (a), 3D solution for minimum structural compliance with fluid velocity streamlines (b), and different views of 3D optimized structure (c) under laminar flow load.
Future Research
The methodology presented here can be used to perform topology optimization on other multiphysics interactions as well.
Currently, the researchers are working on a new project to develop fluid topology optimization with the same method. “What we are doing is very simple. The procedure is divided into two parts,” said Ranjbarzadeh. First, they are solving a CFD problem using COMSOL Multiphysics. “We define the geometry, meshing, and calculate the sensitivity analysis.” Next, they deliver the sensitivity to a grid of optimization points in MATLAB® (the TOBS method was written in the MATLAB® environment). From there, the team calculates and analyzes the topology optimization. The process is repeated until the optimization problem is solved.
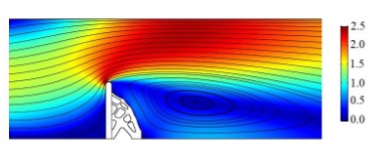
Ongoing research involving FSI topology optimization solution for minimum structural compliance with fluid velocity streamlines under a turbulent flow load (Note: paper is under revision).
Reference
- S. Ranjbarzadeh, R. Picelli, R. Sivapuram, R. S. Gioria, E. C. N. Silva, “Topology optimization of binary structures under design-dependent FSI loads“, Structural and Multidisciplinary Optimization, vol. 62, pp. 2101–2116, 2020.
- Sivapuram, R. Picelli, “Topology optimization of binary structures using Integer Linear Programming”, Finite Elements in Analysis and Design, vol. 139, pp. 49–61, 2018.
MATLAB is a registered trademark of The MathWorks, Inc.







Comments (4)
SME Coils
May 21, 2021This is great and superb post. Thanks for providing informative post.
Kirttayoth Yeranee
June 16, 2021Could you share the .mph file (version < 5.5) ? so that I could learn directly from the file.
Rachel Keatley
June 17, 2021Hi Kirttayoth Yeranee,
Thank you for your comment! This model file is not currently available for download, as it is from customer research.
Best,
Rachel
Mervenaz Sahin
March 20, 2024Can you please provide the reference for the ‘3D FSI Topology Optimization’ case, I couldn’t find that model on internet. Thanks!