In the wave optics field, it is difficult to simulate large optical systems in a way that rigorously solves Maxwell’s equation. This is because the waves that appear in the system need to be resolved by a sufficiently fine mesh. The beam envelope method in the COMSOL Multiphysics® software is one option for this purpose. In this blog post, we discuss how to use the Electromagnetic Waves, Beam Envelopes interface and handle its restrictions.
Comparing Methods for Solving Large Wave Optics Models
In electromagnetic simulations, the wavelength always needs be resolved by the mesh in order to find an accurate solution of Maxwell’s equations. This requirement makes it difficult to simulate models that are large compared to the wavelength. There are several methods for stationary wave optics problems that can handle large models. These methods include the so-called diffraction formulas, such as the Fraunhofer, Fresnel-Kirchhoff, and Rayleigh-Sommerfeld diffraction formula and the beam propagation method (BPM), such as paraxial BPM and the angular spectrum method (Ref. 1).
Most of these methods use certain approximations to the Helmholtz equation. These methods can handle large models because they are based on the propagation method that solves for the field in a plane from a known field in another plane. So you don’t have to mesh the entire domain, you just need a 2D mesh for the desired plane.
Compared to these methods, the Electromagnetic Waves, Beam Envelopes interface in COMSOL Multiphysics (which we will refer to as the Beam Envelopes interface for the rest of the blog post) solves for the exact solution of the Helmholtz equation in a domain. It can handle large models; i.e., the meshing requirement can be significantly relaxed if a certain restriction is satisfied.

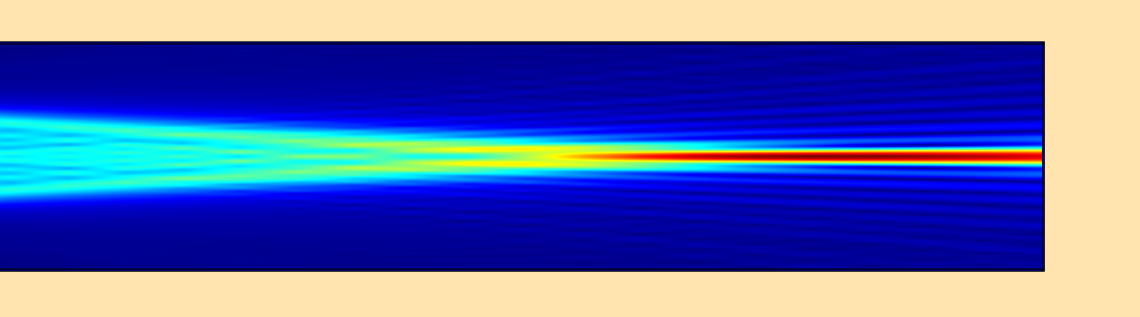
A beam envelopes simulation for a lens with a millimeter-range focal length for a 1-um wavelength beam.
We discuss the Beam Envelopes interface in more detail below.
Theory Behind the Beam Envelopes Interface
Let’s take a look at the math that the Beam Envelopes interface computes “under the hood”. If you add this interface to a model and click the Physics Interface node and change Type of phase specification to User defined, you’ll see the following in the Equation section:
Here, \bf E1 is the dependent variable that the interface solves for, called the envelope function.
In the phasor representation of a field, \bf E1 corresponds to the amplitude and \phi_1 to the phase, i.e.,
The first equation, the governing equation for the Beam Envelopes interface, can be derived by substituting the second definition of the electric field into the Helmholtz equation. If we know \phi_1, the only unknown is \bf E1 and we can solve for it. The phase, \phi_1, needs to be given a priori in order to solve the problem.
With the second equation, we assume a form such that the fast oscillation part, the phase, can be factored out from the field. If that’s true, the envelope \bf E1 is “slowly varying”, so we don’t need to resolve the wavelength. Instead, we only need to resolve the slow wave of the envelope. Because of this process, simulating large-scale wave optics problems is possible on personal computers.
A common question is: “When do you want the envelope rather than the field itself?” Lens simulation is one example. Sometimes you may need the intensity rather than the complex electric field. Actually, the square of the norm of the envelope gives the intensity. In such cases, it suffices to get the envelope function.
What Happens If the Phase Function Is Not Accurately Known?
The math behind the beam envelope method introduces more questions:
- What if the phase is not accurately known?
- Can we use the Beam Envelopes interface in such cases?
- Are the results correct?
To answer these questions, we need to do a little more math.
1D Example
Let’s take the simplest test case: a plane wave, Ez = \exp(-i k_0 x), where k_0 = 2\pi / \lambda_0 for wavelength \lambda_0 = 1 um, it propagates in a rectangular domain of 20 um length. (We intentionally use a short domain for illustrative purposes.)
The out-of-plane wave enters from the left boundary and transmits the right boundary without reflection. This can be simulated in the Beam Envelopes interface by adding a Matched boundary condition with excitation on the left and without excitation on the right, while adding a Perfect Magnetic Conductor boundary condition on the top and bottom (meaning we don’t care about the y direction).
The correct setting for the phase specification is shown in the figure below.
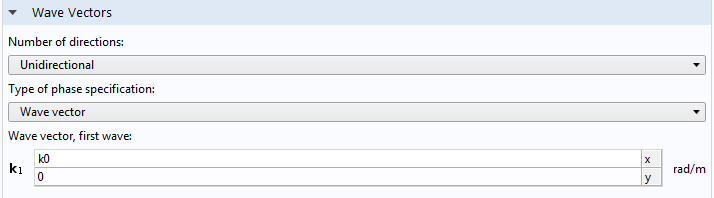
We have the answer Ez = \exp(-i k_0 x), knowing that the correct phase function is k_0 x or the wave vector is (k_0,0) a priori. Substituting the phase function in the second equation, we inversely get E1z = 1, the constant function.
How many mesh elements do we need to resolve a constant function? Only one! (See this previous blog post on high-frequency modeling.)
The following results show the envelope function \bf E1 and the norm of \bf E, ewbe.normE, which is equal to |{\bf E1}|. Here, we can see that we get the correct envelope function if we give the exact phase function, constant one, for any number of meshes, as expected. For confirmation purposes, the phase of \bf E1z, arg(E1z), is also plotted. It is zero, also as expected.

The envelope function (red), the electric field norm (blue), and the phase of the envelope function (green) for the correct phase function k0x, computed for different mesh sizes.
Now, let’s see what happens if our guess for the phase function is a little bit off — say, (0.95k_0,0) instead of the exact (k_0,0). What kind of solutions do we get? Let’s take a look:

The envelope function (red), the electric field norm (blue), and the phase of the envelope function (green) for the wrong phase function, 0.95 k0x, computed for different mesh sizes.
What we see here for the envelope function is the so-called beating. It’s obvious that everything depends on the mesh size. To understand what’s going on, we need a pencil, paper, and patience.
We knew the answer was Ez = \exp(-i k_0 x), but we had “intentionally” given an incorrect estimate in the COMSOL® software. Substituting the wrong phase function in the second equation, we get \exp(-i k_0 x)={\bf E1z} \exp(-0.95i k_0 x). This results in {\bf E1z} = \exp(-0.05i k_0 x), which is no longer constant one. This is a wave with a wavelength of \lambda_b= 2\pi/0.05k_0 = 20 um, which is called the beat wavelength.
Let’s take a look at the plot above for six mesh elements. We get exactly what is expected (red line), i.e., {\bf E1z} = \exp(-0.05i k_0 x). The plot automatically takes the real part, showing {\bf E1z} = \cos(-0.05 k_0 x). The plots for the lower resolutions still show an approximate solution of the envelope function. This is as expected for finite element simulations: coarser mesh gives more approximate results.
This shows that if we make a wrong guess for the phase function, we get a wrong (beat-convoluted) envelope function. Because of the wrong guess, the envelope function is added a phase of the beating (green line), which is -0.05 k_0 x.
What about the norm of \bf E? Look at the blue line in the plots above. It looks like the COMSOL Multiphysics software generated a correct solution for ewbe.normE, which is constant one. Let’s calculate: Substituting both the wrong (analytical) phase function and the wrong (beat-convoluted) envelope function in the second equation, we get {\bf Ez} = \exp(-0.05i k_0 x) \times \exp(-0.95i k_0 x) = \exp(-i k_0 x), which is the correct fast field!
If we take a norm of \bf E, we get a correct solution, constant one. This is what we wanted. Note that we can’t display \bf E itself because the domain can be too large, but we can find \bf E analytically and display the norm of \bf E with a coarse mesh.
This is not a trick. Instead, we see that if the phase function is off, the envelope function will also be off, since it becomes beat-convoluted. However, the norm of the electric field can still be correct. Therefore, it is important that the beat-convoluted envelope function be correctly computed in order to get the correct electric field. The above plots clearly show that. The six-element mesh case gives the completely correct electric field norm because it fully resolves the beat-convoluted envelope function. The other meshes give an approximate solution to the beat-convoluted envelope function depending on the mesh size. They also do so for the field norm. This is a general consequence that holds true for arbitrary cases.
No matter what phase function we use in COMSOL Multiphysics, we are okay as long as we correctly solve the first equation for \bf E1 and as long as the phase function is continuous over the domain. When there are multiple materials in a domain, the continuity of the phase function is also critical to the solution accuracy. We may discuss this in a future blog post, but it is also mentioned in this previous blog post on high-frequency modeling.
2D Example
So far, we have discussed a scalar wave number. More generally, the phase function is specified by the wave vector. When the wave vector is not guessed correctly, it will have vector-valued consequences. Suppose we have the same plane wave from the first example, but we make a wrong guess for the phase, i.e., k_0(x \cos \theta + y \sin \theta) instead of k_0 x . In this case, the wave number is correct but the wave vector is off. This time, the beating takes place in 2D.
Let’s start by performing the same calculations as the 1D example. We have \exp(-i k_0 x)= {\bf E1z}(x,y) \exp(-i k_0 (x \cos \theta+y \sin \theta) ) and the envelope function is now calculated to be {\bf E1z}(x,y) = \exp(-i k_0 (x (1-\cos \theta) -y \sin \theta) ) , which is a tilted wave propagating to direction (1-\cos \theta, -\sin \theta) , with the beat wave number k_b = 2 k_0/\sin (\theta/2) and the beat wavelength \lambda_b=\lambda_0/(2\sin (\theta/2)).
The following plots are the results for θ = 15° for a domain of 3.8637 um x 29.348 um for different max mesh sizes. The same boundary conditions are given as the previous 1D example case. The only difference is that the incident wave on the left boundary is {\bf E1z}(0,y) = \exp(i k_0 y \sin \theta) . (Note that we have to give the corresponding wrong boundary condition because our phase guess is wrong.)
In the result for the finest mesh (rightmost), we can confirm that \bf E1z is computed just like we analyzed in the above calculation and the norm of \bf Ez is computed to be constant one. These results are consistent with the 1D example case.

The electric field norm (top) and the envelope function (bottom) for the wrong phase function k_0(x \cos\theta +y \sin\theta ), computed for different mesh sizes. The color range represents the values from -1 to 1.
Simulating a Lens Using the Beam Envelopes Interface
The ultimate goal here is to simulate an electromagnetic beam through optical lenses in a millimeter-scale domain with the Beam Envelopes interface. How can we achieve this? We already discussed how to compute the right solution. The following example is a simulation for a hard-apertured flat top incident beam on a plano-convex lens with a radius of curvature of 500 um and a refractive index of 1.5 (approximately 1 mm focal length).
Here, we use \phi_1 = k_0 x, which is not accurate at all. In the region before the lens, there is a reflection, which creates an interference. In the lens, there are multiple reflections. After the lens, the phase is spherical so that the beam focuses into a spot. So this phase function is far different from what is happening around the lens. Still, we have a clue. If we plot \bf E1z, we see the beating.

Plot of \bf E1z. The inset shows the finest beat wavelength inside the lens.
As can be seen in the plot, a prominent beating occurs in the lens (see the inset).
Note: As of version 5.5, the Transition boundary condition was introduced on the lens surfaces to mimic an antireflection coating, which eliminates the beating due to the reflection. (See this previous blog post. Note also that mesh refinement is necessary even with an antireflection coating because it works only for the normal incidence. The field around the lens edges may have some beating.
Actually, the finest beat wavelength is \lambda_0/2 in front of the lens. To prove this, we can perform the same calculations as in the previous examples. The finest beat wavelength is due to the interference between the incident beam and reflected beam, but we can ignore this because it doesn’t contribute to the forward propagation. We can see that the mesh doesn’t resolve the beating before the lens, but let’s ignore this for now.
The beat wavelength in the lens is 3\lambda_0/2 for the backward beam and 2\lambda_0 for the forward beam for n = 1.5, which we can also prove in the same way as the previous examples. Again, we ignore the backward beam. In the plot, what’s visible is the 2\lambda_0 beating for the forward beam. The backward beam is only a fraction (approximately 4% for n = 1.5 of the incident beam, so it’s not visible). The following figure shows the mesh resolving the beat inside the lens with 10 mesh elements.
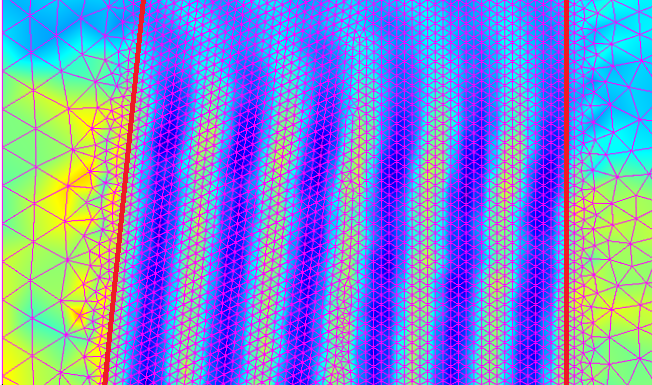
The beat wavelength inside the lens. The mesh resolves the beat with 10 mesh elements.
Other than the beating for the propagating beam in the lens, the beating in the subsequent air domain is pretty large, so we can use a coarse mesh here. This may not hold for faster lenses, which have a more rapid quadratic phase and can have a very short beat wavelength. In this example, we must use a finer mesh only in the lens domain to resolve the fastest beating.
The computed field norm is shown at the top of this blog post. To verify the result, we can compute the field at the lens exit surface by using the Frequency Domain interface, and then using the Fresnel diffraction formula to calculate the field at the focus. The result for the field norm agrees very well.
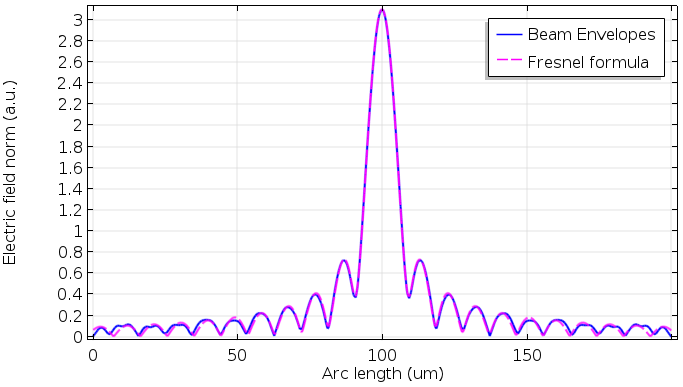
Comparison between the Beam Envelopes interface and Fresnel diffraction formula. The mesh resolves the beat inside the lens with 10 mesh elements.
The following comparison shows the mesh size dependence. We get a pretty good result with our standard recommendation, \lambda_b/6, which is equal to \lambda_0/3. This makes it easier to mesh the lens domain.
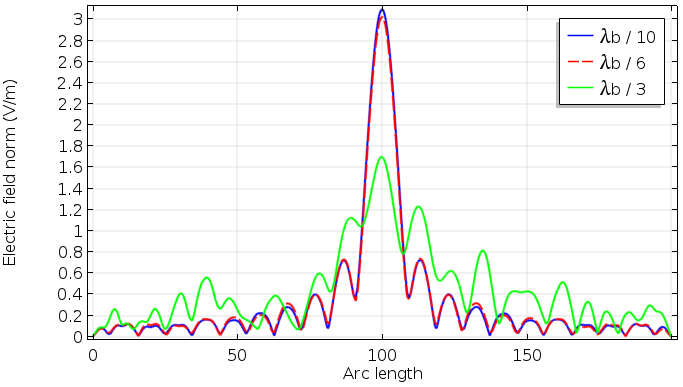
Mesh size dependence on the field norm at the focus.
As of version 5.3a of the COMSOL® software, the Fresnel Lens tutorial model includes a computation with the Beam Envelopes interface. Fresnel lenses are typically extremely thin (wavelength order). Even if there is diffraction in and around the lens surface discontinuities, the fine mesh around the lens part does not significantly impact the total number of mesh elements.
Concluding Remarks
In this blog post, we discuss what the Beam Envelopes interface does “under the hood” and how we can get accurate solutions for wave optics problems. Even if we get beating, the beat wavelength can be much longer than the wavelength, which makes it possible to simulate large optical systems.
Although it seems tedious to check the mesh size to resolve beating, this is not extra work that is only required for the Beam Envelopes interface. When you use the finite element method, you always need to check the mesh size dependence for accurately computed solutions.
Next Steps
Try it yourself: Download the file for the millimeter-range focal length lens by clicking the button below.
References
- J. Goodman, Fourier Optics, Roberts and Company Publishers, 2005.






Comments (47)
Phillip Springer
January 15, 2018Dear Mr. Yosuke Mizuyama,
I am trying to set COMSOL up to solve the Helmholtz equation in 3D. In my attempt, I basically define a cuboid where one plain shall have an initial electric field distribution and I want to know the electric field at the opposing side. My initial electric field shall be arbitrary, but for test purposes I have it as a Gaussian. This works well, as long as there are no focusing terms. When I use a complex-valued Gaussian, e.g. with a focusing term exp(i*k*(x^2+z^2)/2/R_0) [propagation direction is y], then solution does not look ok. I also tried to use a user-defined phase within the Beam Envelopes interface, but no success either. Can you give me some advice on how to propagate an (arbitrary) initial electric field distribution that may contain a focusing phase in 3D?
Yosuke Mizuyama
January 16, 2018Dear Phillip,
Thank you for reading my blog. It’s a little bit hard to diagnose what went wrong from your problem description but your phase expression seems correct. What I can think of is that you might have used a small domain size compared to the beam width or a small R_0 compared to the wavelength, in which case you need to pay a special attention. I recommend using a large domain size and start from a very large R_0. If you are successful, then you can reduce them.
Best regards,
Yosuke
QASSIM AL-JARWANY
March 16, 2018Hi Yosuke Mizuyama,
I am working with COMSOL version 5.3, I am looking to calculate the electric field underneath the micro particle silica (1um diameter ) was irradiated by ArF laser (193nm) ,please if you have any tutorial about .
Cheers
Qassim
Yosuke Mizuyama
March 16, 2018Dear Qassim,
Thank you for your interest in my blog. I need more information to tell anything but it looks like we don’t have any particular tutorial for your purpose. Please let us know if you have any other questions.
Best regards,
Yosuke
Sildona Ristani
April 30, 2018Dear Yosuke Mizuyama,
Thank you very much for this interesting results.
I want to build a lens to focus a Gaussian beam with wavelength 1.064 µm and beam waist 7*wavelength in RF module.
I am at a starting point and I would highly appreciate some tips.
Thank you very much,
Sildona Ristani
Yosuke Mizuyama
April 30, 2018Dear Sildona,
Thank you for reading my blog. The RF module does not include the Beam Envelopes interface. You can use the Frequency Domain interface in the RF module instead since your beam size seems to be small enough. Please note these two tips: 1. Resolve the mesh for the high frequency wave in order to get accurate solutions, 2. Use Scattering Boundary Condition for all boundaries to allow the reflection from the lens surfaces to go out.
I hope your simulation goes well.
Best regards,
Yosuke
Safoura N
July 20, 2018Dear Mr. Mizuyama,
Thank you for the interesting and clearly explained blog.
I am using electromagnetic wave frequency domain interference, I want to simulate diffraction pattern in far filed. As you know, millimeter-size cannot be simulated with the Frequency Domain interface because it requires a large number of meshes also the Full-wave simulation requires more DOF. In my simulation, there are multiple materials with different structures (micrometer range) in the main domain.
Are there any alternative solutions instead of extending the far zone domain?
Is it possible to use the beam envelopes method? If yes, how can define the phase function to find the accurate solution?
I really appreciate any help.
Best regards,
Safoura
Yosuke Mizuyama
July 21, 2018Dear Safoura,
Thank you for reading my blog.
Yes, the Beam Envelopes interface may potentially be able to solve your large problem. You had a very good question about the phase function. It’s very important the the phase function be “continuous” across the domain in addition to the technique that I described in this blog post. This is crucial to the solution accuracy when you have multiple different materials with a different index in your domain in particular.
Please read this blog post:
https://www.comsol.jp/blogs/comparing-two-interfaces-for-high-frequency-modeling/
This blog post includes the simplest example demonstrating how to make the phase function continuous across a material interface.
The “Field continuity” feature will also work more easily (to be able to see the feature, you have to turn on “Advanced Physics Options” in the eye icon pull-down menu in the Model Builder pane).
The setting is a little bit difficult but it’s worth trying!
Please let our support know if you have more questions.
Best regards,
Yosuke
Mohamad reza Aghdaee
January 25, 2019Hello
I want to define a electromagnetic wave that makes a angle with surface and i want to change the angle of incident.please make me know if you can help me
Carolina Rickenstorff
May 2, 2019Carolina Rickenstorff
May 2, 2019Dear Mr. Yosuke,
I followed your video of Fresnel lens simulation and I managed to get it running for the beam envelope method that doesn´t consider the phase mismatch. In my case I simulated a long taper fiber 700um long and 1.55 wvl sorrounded by a medium with refractive index n_medium<n_fiber. What can I do in order to plot the transmitted power in the output plane versus the input plane?
Thanks in advance.
Carolina R
Yosuke Mizuyama
May 2, 2019Dear Carolina,
Thank you for watching my video. Did you use the Port boundary condition for the input and output boundaries? If so, there is a built-in variable called ewbe.Ttotal. You can calculate the value in the Derived Values->Global Evaluation under the Results node or if you sweep some parameters, you can also plot it by using the variable. Am I answering your question?
Best regards,
Yosuke
Jian Wang
January 31, 2020Dear Yosuke
Thanks for your useful and informative blog.
Many thanks
Jian
Carolina Rickenstorff
May 2, 2019Dear Mr. Yosuke,
The port I must choose is user defined isn’t? Do I have to add a mode analysis study or it is not required to get the ewbe.Ttotal variable?
Best regards.
Carolina R
Yosuke Mizuyama
May 2, 2019Dear Carolina,
I need to take a look at your model but most likely you need to choose “Numeric” in the Port properties setting and need to add a Boundary Mode Analysis study step for each input and output port if it’s a tapered core waveguide and you don’t know the boundary mode in advance. If you know the boundary mode shape in advance, you can choose “User Defined” and enter the expression. You don’t need the Boundary Mode Analysis study step in that case.
Best regards,
Yosuke
Carolina Rickenstorff
May 2, 2019Dear Mr. Yosuke,
Indeed my model corresponds to a taper fiber. I’m glad to share my model but how I upload it?
I´m interested in studying the evanescent and to measure the transmission of the fiber but I’m not sure if my results are correct.
Carolina R
Carolina Rickenstorff
May 2, 2019evanescent field
Yosuke Mizuyama
May 3, 2019Dear Carolina,
Yes. Are you a trial user or do you or does your organization have a valid COMSOL license? If so, you can submit your file to support@comsol.com with a note that you would like me to take care of this case.
Best regards,
Yosuke
Carolina Rickenstorff
May 3, 2019Dear Mr. Yosuke,
I’m a trial user.
I’ll try to send you my model by e-mail. As I told you before I’m interested in observing the evanescent field and the fiber transmittance but my model shows a very large tail in the taper region and I don’t know if my results are correct.
Also there´s a conflict with the scattering boundary condition and the numeric ports.
Best regards and thanks for your attention.
Carolina R
Yosuke Mizuyama
May 3, 2019Dear Carolina,
Ok. I will take a look.
Best regards,
Yosuke
Carolina Rickenstorff
May 3, 2019Hello Mr Yosuke,
My request is not accepted. I’m not a trial user. How do I get a trial passcode?
Thanks anyway.
Carolina R
Yosuke Mizuyama
May 3, 2019Hi Carolina,
Please try to reach out to our sales: info@comsol.com.
Best regards,
Yosuke
Carolina Rickenstorff
May 6, 2019Good day Mr. Yosuke, I’ve got a trial licence Nr. 9FFF3FFFF7F53-PYUS-190520-3079429-61556774181E.
I send to you my model looking for your advice.
Regards.
Carolina R
Carolina Rickenstorff
May 6, 2019Hi Mr. Yosuke,
I’m now a trial user. I sent to support@comsol.com with attention to you my model looking for your advice.
Regards.
Carolina R
Yosuke Mizuyama
May 6, 2019Dear Carolina,
Great! Thank you. I will take a look.
Best regards,
Yosuke
Carolina Rickenstorff
May 9, 2019Hello Mr. Yosuke,
What is your diagnostic of my model? Is it normal the long tail of light coming from the taper region? Is it a evanescent wave?
Best regards.
Carolina Rickenstorff
Vladimir Osipov
July 20, 2019Dear Mr. Yosuke Mizuyama,
I’m trial user ans trying to be confirmed that Wave Optics module can be applied for modelling of phase plate, transforming free space Gaussian beam into optical vortex. Could You please add You comments to the solution of this task?
Best regards
Vladimir Osipov
Yosuke Mizuyama
July 21, 2019Dear Vladimir,
Thank you for reading my blog and for being a trial user!
Yes. It is possible to use the Wave Optics module for simulating transforming optics for Gaussian beam to Laguerre Gaussian beam conversion. The familiar spiral diffractive optics for optical vortex may be simulated in a similar way to this example: https://www.comsol.com/model/fresnel-lens-46571. Please try it out.
Best regards,
Yosuke
Vladimir Osipov
July 21, 2019Dear Mr. Yosuke,
Thank You very much for Your recommendations.
Kind wishes
Vladimir
Yosuke Mizuyama
July 22, 2019Dear Vladimir,
You are welcome!
Yosuke
Ahmed Elsharabasy
May 30, 2020Dear Yosuke,
Many thanks for your support in bringing these interesting applications out using COMSOL in this photonics and optics fields.
I’m working on modeling a 2×2 and 4×4 multimode interference (MMI) coupler using the example presented in the following paper: https://cdn.intechopen.com/pdfs/60915.pdf
1) I was wondering how to define the boundary conditions and ports in 2D and 3D. What I did is the following I added numeric ports with one ON and others are OFF. In the 2D model, I used scattering boundary conditions surrounding the multimode waveguide.
2) Do you expect that there’s a significant difference in accuracy between 2D and 3D simulation models?
Thanks,
Ahmed
Yosuke Mizuyama
May 30, 2020 COMSOL EmployeeDear Ahmed,
Thank you for reading my blog.
Your setting seems to be fine. 3D simulations are always more difficult than 2D. Finding a right boundary mode is more difficult. Meshing is difficult too and you run out of memory. The accuracy all depends on how you can overcome these difficulties.
Best regards,
Yosuke
Ahmed Elsharabasy
June 1, 2020Dear Yosuke,
Thanks for your reply.
I wonder whether you’ll add new photonics design models to the application gallery, as I think COMSOL has the ability to lead in photonics as well as other CFD and RF applications. The only main drawback is the lack of supportive models to help researchers/engineers to benefit from.
Just another favor, could you please check if you or anyone in the team can simulate the MMI coupler in the paper I mentioned previously or any other similar example to investigate the appropriate sources and boundary conditions that have to be implemented.
Best,
Ahmed
Farzaneh Ab.
September 25, 2020Dear Yosuke,
Thank you very much for the interesting topic you’ve shared on your blog. I actually went through your webinar talk regarding the beam envelope method for waveguide design in COMSOL Multiphysics too.
Based on your explanation on your talk, in waveguide design when we use the port boundary condition (with Numeric type) and boundary mode analysis (under the study node), then the β_⊥ can be calculated when the boundary mode calculated. And, the longitudinal propagation constant β_∥ is analytically calculated by this formula: k^2=(n_core^2)/C^2 ω^2=β_⊥^2+β_∥^2. Where β_∥^ is actually the ewbe. β_1 that we are defining in Electromagnetic Waves, Beam Envelopes setting under the Wave vector.
Now, when you define the boundary mode (for example a gaussian EH11 with arbitrary width) through the matched boundary condition, then how the transverse propagation β_⊥ is computed? Because in this case, we are not putting any Boundary Mode Analysis under the study node.
How Comsol can handle the wave vector or phase function in a situation where we define an arbitrary transverse mode for the waveguide input (instead of letting the COMSOL compute the transverse mode in Boundary Mode analysis)?
Regards,
Farzaneh
Yosuke Mizuyama
September 26, 2020 COMSOL EmployeeDear Farzaneh,
Thank you for reading my blog and for attending my webinar.
The transverse propagation constant is always determined by the eigenvalue solution in the transverse plane.
When dealing with waveguides, we assume that the transverse direction is somewhat spatially constrained by metals or index jumps,
where only discrete wave numbers are allowed. In COMSOL, if you know the mode type, say, EH11 or whatever, the mode shape and β_⊥ is analytically known from the formulas. COMSOL calculates β_⊥ for your waveguide width using the formulas. This is how β_⊥ is computed without solving any eigenvalue problem for the transverse mode.
On the other hand, if your transverse mode is not known as a formula, then you always need the boundary mode analysis. Otherwise COMSOL won’t know β_⊥, and neither is β_∥.
I hope it helps.
Thanks for your question. It’s a good question for all users.
Best regards,
Yosuke
Farzaneh Ab.
September 28, 2020Dear Yosuke
Thank you for your reply. Very insightful comments!
I need to know more details about this subject and how to apply it in my modeling problem.
I have submitted a new support case with a note that I would like you to take care of this case. Please feel free If you think the case should be forwarded to your other colleagues since I am not aware of the regulations. Many thanks!
Best regards,
Farzaneh
Yosuke Mizuyama
September 29, 2020 COMSOL EmployeeDear Farzaneh,
Of course.
Talk to you later.
Best regards,
Yosuke
azie arif
November 18, 2020Dear Mr. Yosuke Mizuyama,
I have tried and watch the simulation of bend fiber. I want to know about k1.. I have made 2 of u-shape and only one shape can run. i use ewbe.beta_1*radius*atan2(x,-y).. So, the question is, why the second u-shape have nothing response?
I also, interested to know about ewbe.beta_1*r, which is r refer to the direction of beta. am I right?
Regards.
Azie
Emmanuel Marin
March 16, 2021Dear Mr. Yosuke Mizuyama,
I want to simulate the polarization effect in waveguide (e.g. optical fiber) that has a circular birefringence properties in the core or the cladding. I can adjust the efficiency of the circular birefringence by changing coefficients in permittyvity tensor. But I don’t know how to change the input polarization state at the input of my waveguide. The Beam Envelopes Method looks perfect to simulate the propagation, I did not succeed to change the polarization at the input port. Do you have an idea, how I could do this?
Thank you in advance
Emmanuel
Yosuke Mizuyama
March 19, 2021 COMSOL EmployeeDear Emmanuel,
Thank you for reading my blog. If you use the Port feature, you can express arbitrary electric field input by choosing the User defined option.
Thank you.
Yosuke
Peng W
April 17, 2021Dear Mr. Yosuke Mizuyama,
I’ve watched a webinar given by you with the topic of ‘Simulating Optical Waveguides with COMSOL Multiphysics’. In that webinar you mentioned an example of simulating ‘tapered waveguide’. I’d just like to ask if there is a mph file for this simulation. Recently, I was doing simulation on grating couplers. I’m not sure about the correct way to excite a proper mode before the light enters the grating region. I think that is very similar to the case of ‘tapered waveguide’ where the refractive index along the longitudinal direction is not constant. Therefore, it would great if I could have an example mph file of the tapered waveguide as a reference. I’ve tried to find it on COMSOL’s website but failed. So I’m wondering if that’s just an demonstrative file created by you and hasn’t been uploaded onto the website? Looking forward to your reply. Thanks.
Best regards
Yisbel Marin
January 10, 2022In the application files for the focusing lens example for plotting the FD+Fresnel formula formula, there is a factor of 3/2.5 in front of the equation. It is not clear to me where this comes from considering the Fresnel formula. Could you please clarify this? Thank you.
Yosuke Mizuyama
January 11, 2022 COMSOL EmployeeHi Yisbel,
Thank you for reading my blog.
Yes, there was that factor before.
I think it was replaced by the original Fresnel formula’s normalization factor as it is.
Please check the latest version.
Best regards,
Yosuke
Christophe YE
May 31, 2022Dear Mr. Yosuke Mizuyama,
Thank you very much for the information on this blog. I have seen your webinar talk about the beam envelope method for waveguide design in COMSOL Multiphysics and I don’t understand how COMSOL is able to show solution with 1, 2 or X number of modes. Indeed, we have already fixed the geometric parameters and the indexes of the waveguide and also the wavelength so on which parameters COMSOL plays to modify the number of modes ?
Best regards,
Christophe
Yosuke Mizuyama
June 1, 2022 COMSOL EmployeeDear Christophe,
Thank you for reading my blog.
I’m not sure I understand your question.
Please send your question to support@comsol.com with your model file.
Thank you.
Best regards,
Yosuke
静 陈
March 17, 2024Dear Mizuyama-San,
Thanks for this great blog which is very helpful for BEM beginner.
However, I notice there is difference between the variables “ewbe.E1z” and “E1z”, where “E1z” is the envelop field while “ewbe.E1z” is not.
I thought when I use “ewbe” as a prefix from the interface name, the variant should be more accurate, but it seems to mean something else.
It would be much appreciated if you could help to explain the difference between these two variables.
Yosuke Mizuyama
March 17, 2024 COMSOL EmployeeHello,
Thank you for reading my blog.
That’s a good catch.
E1z and ewbe.E1z are both a variable name used in COMSOL.
E1z is the z component of the envelope function and ewbe.E1z is the z component of the electric field.
The relation between these two variables is
ewbe.E1z = E1z*ewbe.expPhi1,
where ewbe.expPhi1 is the phase function.
Please let me know if you have any further questions.
Best regards,
Yosuke