Modeling acoustically large problems requires a memory-efficient approach like the discontinuous Galerkin method. To make solving these types of problems easier, we’ve added a new physics interface based on this method to the Acoustics Module: the Convected Wave Equation, Time Explicit interface. It can include a stationary background flow and is suited for modeling linear ultrasound applications. Today, we will explore how to use this interface with the example of an ultrasound flow meter.
About the Convected Wave Equation, Time Explicit Physics Interface
The new Convected Wave Equation, Time Explicit interface builds on the functionality of the Acoustics Module. The technology behind this interface comes from the discontinuous Galerkin (DG) method, also called DG-FEM, which relies on a solver that is time explicit and very memory lean. Using the Convected Wave Equation, Time Explicit interface enables you to efficiently solve large transient linear acoustics problems that contain many wavelengths in a stationary background flow. It also includes absorbing layers (sponge layers) that can act as effective nonreflecting boundary conditions.
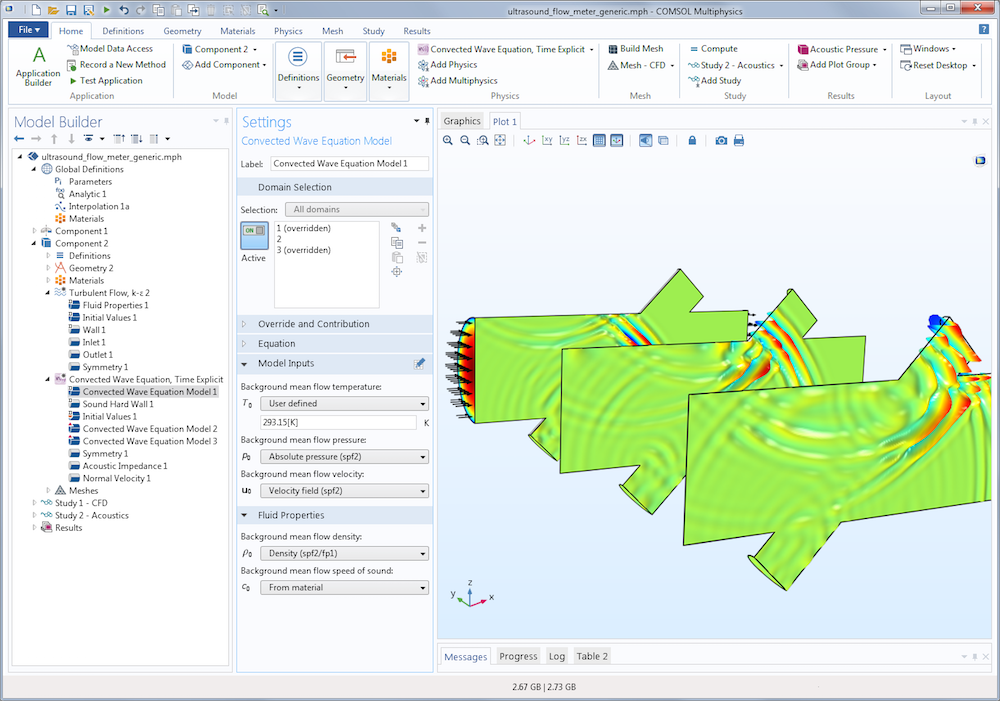
A model of an ultrasound flow meter that uses the Convected Wave Equation, Time Explicit interface. A turbulent flow model is also present to calculate the background flow through the flow meter.
With the absorbing layer technology to truncate the computational domain and the memory-efficient formulation of DG-FEM, you can set up and solve very large problems in the time domain — measured in terms of the number of wavelengths that can be resolved. This makes the Convected Wave Equation, Time Explicit interface suited for modeling the propagation of linear acoustic signals that span large distances in relation to the wavelength.
This interface is useful for linear ultrasound applications, such as ultrasound flow meters and ultrasound sensors in which the time-of-flight parameter is considered. It is also useful for nonultrasound applications like room acoustics and auto cabins that experience the transient propagation of audio pulses.
Solving the Linearized Euler Equations
The governing equations solved by the Convected Wave Equation, Time Explicit interface are the linearized Euler equations. These equations assume an adiabatic equation of state (see Ref. 1 and Ref. 2). The mass and momentum conservation equations read:
& \frac{\partial \rho}{\partial t}+\nabla\cdot(\rho \mathbf{u}_0 + \rho_0 \mathbf{u})=0 \\
& \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}_0\cdot\nabla)\mathbf{u} + (\mathbf{u}\cdot\nabla)\mathbf{u}_0 + \frac{1}{\rho_0}\nabla p -\frac{\rho}{\rho_0^2}\nabla p_0 = 0 \\
& p=c_0^2 \rho
\end{align}
The acoustic pressure p, as well as the acoustic velocity perturbation u, are the dependent variables. The speed of sound is c0 and the steady-state mean background flow variables are defined with a subscript 0 through the density ρ0, pressure p0, and velocity field u0.
The background flow can be a stationary flow with a velocity gradient that ranges from small to moderate. When the background velocity is set to zero, the equations are effectively reduced to modeling the classical wave equation. Note that there are no physical loss mechanisms in the interface and the above equations are set on a conservative form.
Increasing Efficiency with a Time-Explicit Method
The Convected Wave Equation, Time Explicit interface is, as mentioned, based on the DG method, a time-explicit formulation that is memory efficient. With this method, it isn’t necessary to invert a full system matrix when stepping forward in time. In contrast, time-implicit methods require inverting this matrix, which consumes a lot of memory when solving large problems. In DG-FEM, only a few mass matrices are inverted for a reference mesh element (making them small in size) before evolving in time. The method is also quadrature free. As for the DG method, computing the local flux vector and divergence of the flux is a time-consuming process that can be run efficiently with BLAS level 3 operations.
Implicit methods are sometimes thought to be faster on small to medium problems that fit in the RAM. This is not always true. When doing a comparison, it’s important to look at the error level. When using an implicit method, it’s tempting to use a time step that is too large, which introduces errors from the time method. On the other hand, due to the discontinuous elements, the DG method is more accurate for the same polynomial order and mesh.
The FEM-based physics interfaces, such as the Pressure Acoustics, Transient or Linearized Navier-Stokes, Transient interfaces, require the use of a time-implicit method. The challenge is that the RAM consumption for implicit methods grows rapidly when increasing the model size or frequency. The latter is due to the fact that the smallest wavelength in the system must be resolved with a certain number of mesh elements. Still, FEM methods are more flexible and can easily be coupled in multiphysics applications.
In its default formulation, the Convected Wave Equation, Time Explicit interface uses quartic (fourth-order) shape functions, a sweet spot for speed and efficiency in wave problems solved with the DG method. This allows us to use a mesh with an element size that is about half of the wavelength for the highest-frequency component that needs to be resolved. This in turn simplifies meshing for large problems.
As an example, the ultrasound flow meter model presented below consists of 7.6 million degrees of freedom (DOF) and can be solved on a desktop computer using 9.5 GB of RAM. With an implicit formulation, solving a model of this size on a desktop is inconceivable. The solution time depends less on the RAM available and more on the processor speed and number of cores available, as the code runs fully parallelized. The DG-FEM formulation is very well suited for parallelization.
In the Acoustics Module, COMSOL plans to use the DG-FEM formulation more in the future, as we believe it is truly effective for solving large wave propagation problems. We are also continuously working on improving and fine-tuning the method and solvers.
The Absorbing Layer Feature
As mentioned above, the Convected Wave Equation, Time Explicit interface comes with an Absorbing Layer feature. This is a type of sponge layer similar to the perfectly matched layer (PML) that already exists in many frequency domain interfaces. The difference lies in the technique that the absorbing layer uses — it combines a scaling system, filtering, and a simple low-reflecting impedance condition.
Inside the layer domain, a coordinate scaling effectively reduces the speed of the propagating waves and ensures that they “align up” (normal) toward the outer boundary. This means that the waves hit the outer boundary in a direction that is closer to normal. Filtering attenuates and filters out the wave’s high-frequency components that the scaling generates. At the layer’s outer boundary, a simple plane-wave impedance condition removes all of the remaining waves, since normal incidence has been ensured. The animation below, created using the Gaussian Pulse in 2D Uniform Flow: Convected Wave Equation and Absorbing Layers benchmark tutorial, shows absorbing layers in action.
The time evolution of a Gaussian pulse in a uniform background flow. The flow moves toward the right side at Mach 0.5. The absorbing layers absorb the outgoing waves.
Modeling a Linear Ultrasound Application in COMSOL Multiphysics®
As an application example for the Convected Wave Equation, Time Explicit interface, let’s take a look at an ultrasound flow meter set with a generic, wetted time-of-flight configuration. Wetted ultrasound flow meters have a dedicated signal tube for the ultrasound signal and the whole device is mounted into the tubing where the flow is measured. To estimate the speed of the main flow, we calculate the difference in arrival times for two signals that simultaneously traverse the flow upstream and downstream.
In our model, water fills the flow meter and the main flow tube has a diameter of 5 mm. The image below shows the background flow field when one symmetry condition is used. The average velocity in the main channel is 10 m/s. (Note that simulating the flow requires the CFD Module.) The signal tube is the small side duct sitting at a 45° angle to the main channel.
To learn more about this model, you can find step-by-step instructions in the Application Library.
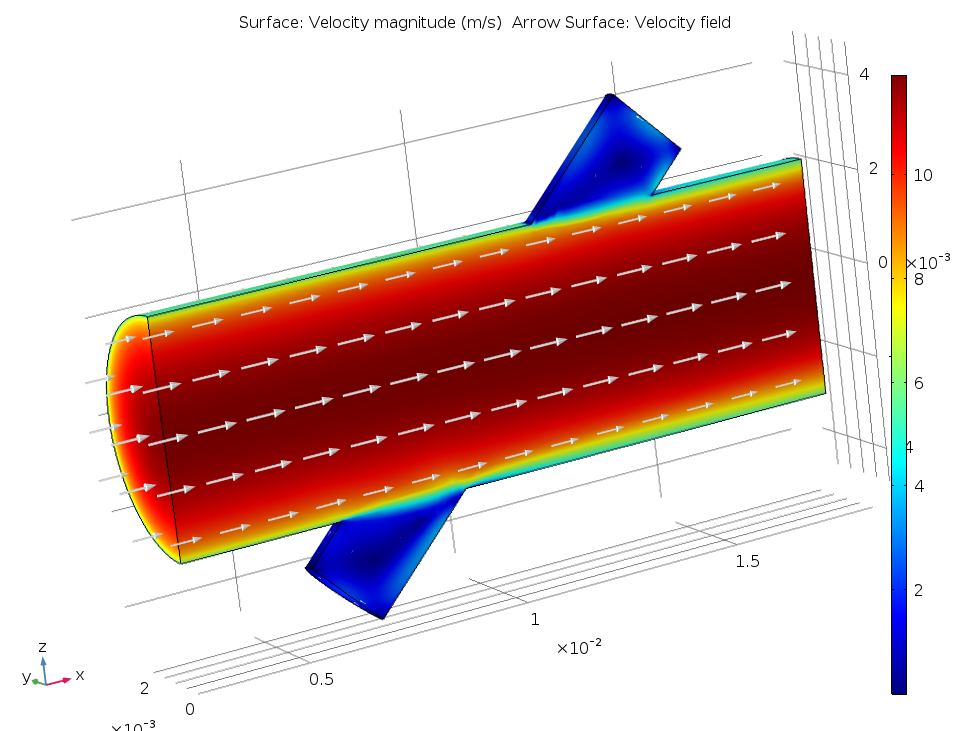
Background mean flow inside the ultrasound flow meter.
The animation below shows the propagation of the acoustic pulse downstream in the signal tube, its interaction with the background flow, and the diffraction effects. The signal is a harmonic carrier at 2.5 MHz with a Gaussian pulse envelope. There are absorbing layers placed at the inlet and outlet of the main duct. The animation only shows the pressure signal magnitude on the symmetry plane of the system. As previously noted, this acoustics model involves solving 7.6 million DOF and can be run on a desktop using 9.5 GB of RAM.
Propagation of the acoustic pulse downstream through the signal tube in the ultrasound flow meter.
The figure below shows the received signals for the pulse propagating upstream (green) and downstream (blue). We measure the arrival time difference between the two signals to be 49 ns and use it to estimate the mean flow velocity, getting a value of 10.75 m/s. While the actual value is 10 m/s, we know that the difference in results is due to the flow profile correction factor (FPCF), an important parameter for this model. Using simulation, we can calculate the value of the FPCF, as the flow field is known a priori from simulations. We can also optimize the flow meter geometry and test different detection signals.
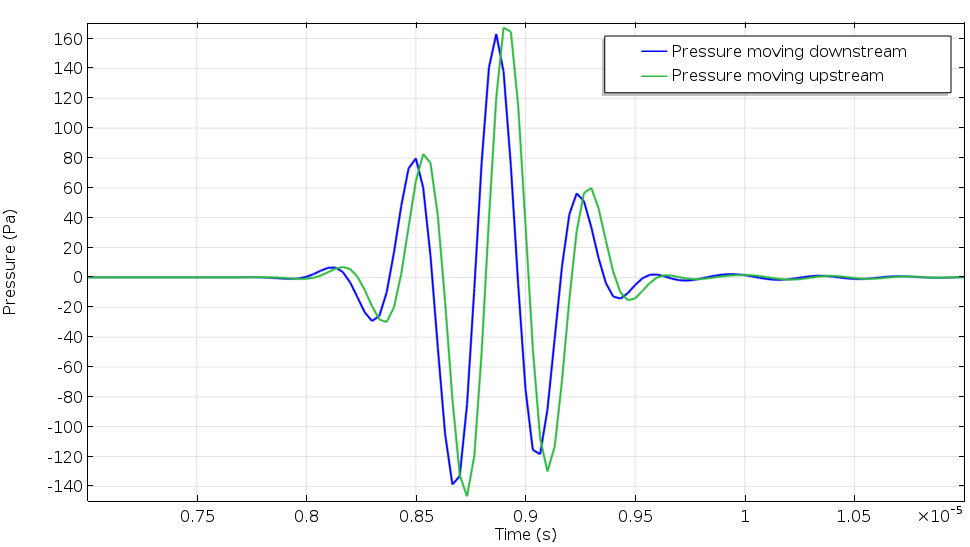
Pressure signal profiles for the signals moving upstream and downstream in the ultrasound flow meter. The arrival time difference is used to predict the mean flow velocity in an ultrasound flow meter.
General Modeling Considerations for the Convected Wave Equation, Time Explicit Interface
Editor’s note: As of COMSOL Multiphysics® version 5.3, a new mesh quality optimization procedure is available to speed up the DG method. This optimization is important to the performance of the method and should be used whenever possible. To learn more, visit the Release Highlights page or see the Acoustics Module user guide.
When using the Convected Wave Equation, Time Explicit interface, based on the DG-FEM formulation, there are certain general modeling considerations that are good to know. Some practices differ from those associated with the FEM-based interfaces in the Acoustics Module. These guidelines are also available in the Acoustics Module User’s Guide under the “Modeling with the Convected Wave Equation Interface” section.
Setting Up Absorbing Layers
The absorbing layer is set up from the Definitions node in the model tree just like a PML — by adding the absorbing layer to the geometric entity that represents the layer. (As for the PML, it is good practice to use the Layers option when creating the geometry of your model.) Once the absorbing layer is set up, we need to place an Acoustic Impedance boundary condition on the outermost boundary of the layer. For advanced users, while the default values usually work well, the filter parameters for the absorbing layer can be modified at the topmost physics level once we enable Advanced Physics Options to be shown.
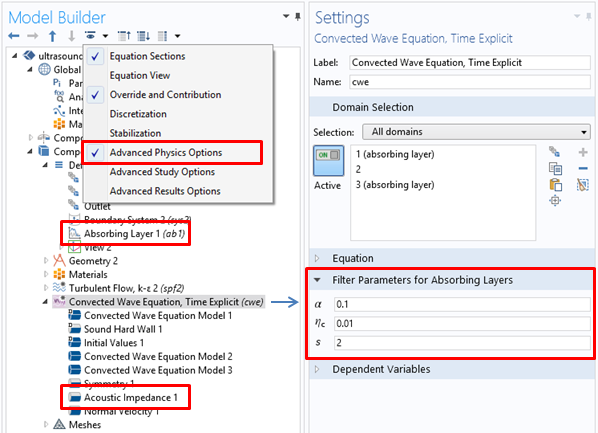
Settings for the Absorbing Layer feature and the Acoustic Impedance boundary condition.
Meshing Models
Meshing a model using the Convected Wave Equation, Time Explicit interface is slightly different than with most other physics interfaces in the Acoustics Module. Since the default settings are for using fourth-order shape functions, we can usually achieve proper spatial resolution with a mesh that has an element size set to anything between λmin/2 and λmin/1.5. Note that the internal time-stepping size of a time-explicit method is strictly controlled by the CFL condition and thus the mesh size. This means that the smallest mesh elements in a model control the time step, so avoiding small mesh elements is a good idea if possible. The internal time step used for the Convected Wave Equation, Time Explicit interface is automatically selected, based on the mesh and physics, by the COMSOL Multiphysics® software.
Storing Data to Reduce Model Size
When solving large transient models that include millions of DOF, the amount of data in the output can be very large and result in stored files of many GBs. A good strategy for reducing the model size is to only store data on the geometric entities that are needed for postprocessing; for example, on a symmetry plane, along a line, or in a point. We can easily accomplish this in COMSOL Multiphysics by using the Store fields in output functionality (located under the Values of Dependent Variables section) in the study step settings. Here, we can decide what selections data has to be stored. Note that the Times specified in the Study Settings section are the times when the solution is stored — they are not related to the internal time stepping.
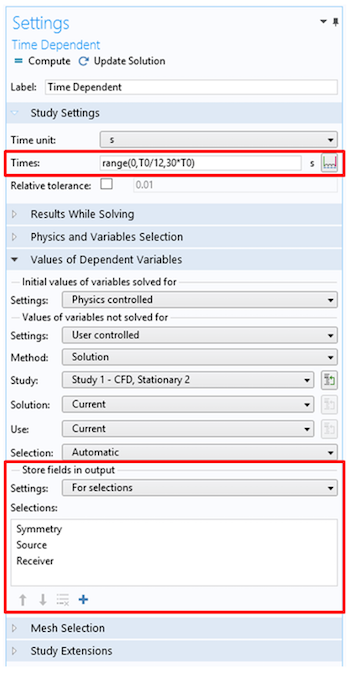
Reducing the size of stored files can be done by setting the times where the solution is stored and saving data only in the selections where you need it.
Postprocessing the Results
When analyzing the results from a simulation run with the Convected Wave Equation, Time Explicit interface, we need to remember that fourth-order elements discretize the dependent variables. This means that within a mesh element, the shape function has a lot of freedom and can contain a lot of spatial details. We can view these details by setting a high Resolution in the Quality section for the plots. When solving a model, the default plots generated already have this option selected, with a custom resolution and the Element refinement set to six. When adding more user-defined plots, we must change the resolution.
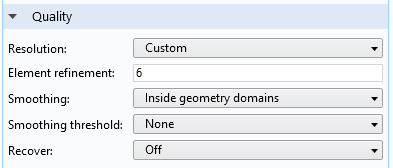
Setting a custom resolution with the Element refinement set to six ensures good spatial representation of solutions.
An example of the difference between the custom resolution set for a default plot and the default resolution for an added user-defined plot is displayed in the figures below. At first glance, it looks like the solution on the left is incorrect. However, once the correct resolution is selected in the Quality section, it reveals the true wave nature of the solution.
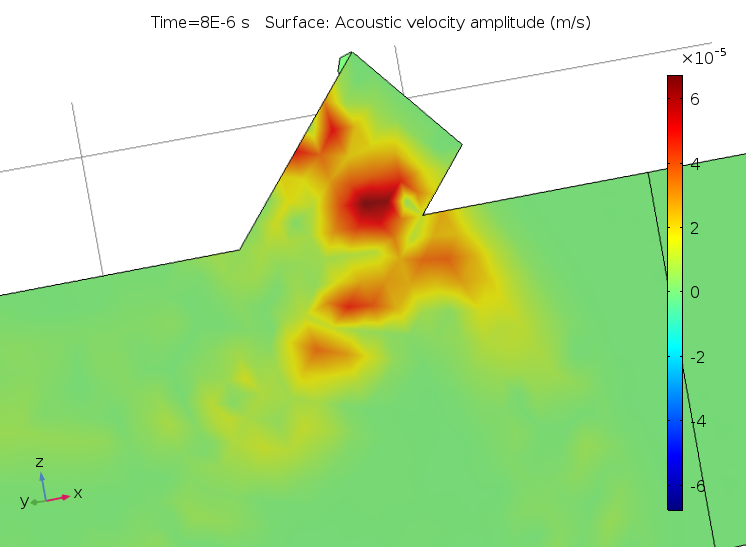
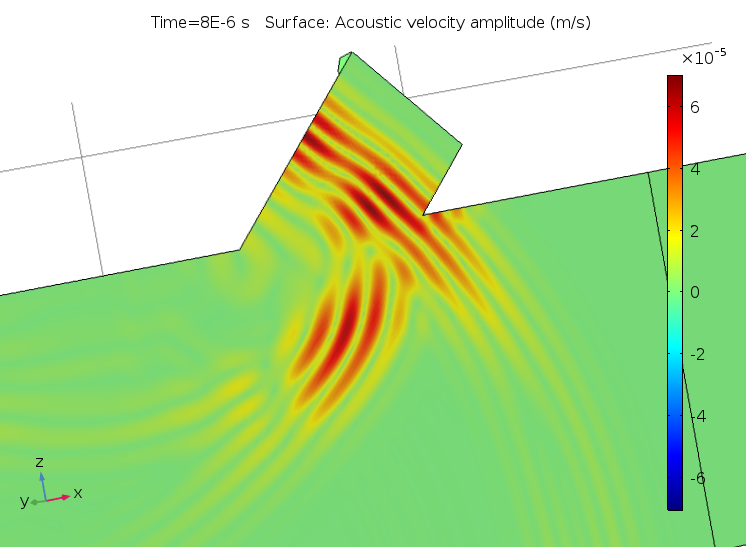
The acoustic velocity with an incorrect resolution (left) and the correctly configured plot with a high resolution (right).
Editor’s note: The performance numbers shown here have improved with the release of COMSOL® 5.3. We will continue to work on improving these numbers in future versions of the software.
Learn More About Modeling Acoustics Applications in COMSOL Multiphysics®
- Download the models highlighted in this blog post:
- Find out how to model other acoustics applications on the COMSOL Blog
- Check out other updates to the Acoustics Module on the Release Highlights page
References
- A. D. Pierce, “Acoustics, An Introduction to its Physical Principles and Applications,” Acoustical Society of America (1991).
- A. D. Pierce, “Wave equation for sound in fluids with unsteady inhomogeneous flow,” The Journal of the Acoustical Society of America. 87, pp. 2292 (1990).




Comments (12)
pengtao huang
March 27, 2017Hi, thanks for sharing you work , i’d like also to build a model under ultrasound effect, but in my 4.4 version, i don’t have “convected wave equation”(cwe) physic, so i’d like to ask how could i build a simple 3D model in 4.4 version?
Best Regards
Mads Jakob Herring Jensen
March 29, 2017Hi, Modeling ultrasound applications in 3D without the new functionality is in most cases not feasible because of the memory requirements of the FEM formulation. This is why we use the very memory efficient DG formulation for the new CWE interface. This is only available in 5.2a. Best regards, Mads
Pengtao Huang
April 3, 2017Thank you for you reply, i’ve find a solution which is similar correct. Define a point load or line load, regard the signal as a force sinusoidal applied in z direction, and choice “Low-reflected boundaries”. I could get a video similar to yours. Now, i’d like to verify this methode
Marcel Remillieux
April 27, 2017Hello Mads,
Could you explain why it is not possible to use DG to solve a problem of elastic wave propagation in a hyperelastic material type Murnaghan (basically acousto-elasticity or nonlinear elasticity). When I try, COMSOL indicates that I should use an implicit solver.
Thanks!
MR
Mads Jakob Herring Jensen
April 27, 2017Dear Marcel
You cannot just switch to an explicit solver for an existing physics. Most physics in COMSOL are based on a finite element formulation of the underlying governing equations. We have formulated the equations specifically for the DG method (in the convected wave equation interface) in order to use the time explicit solver. Not all system of equations, describing physical phenomena, are suited for the DG approach.
Best regards
Mads
Marcel Remillieux
April 28, 2017Thanks, Mads. Any plan to integrate the DG formulation in the Structural Mechanics and Nonlinear Structural Materials modules in the near future? Solving large problems at reduced computational costs in the field of linear and nonlinear elasticity (e.g., seismic waves in geophysics, guided waves in nondestructive testing) is of interest to many people who are currently using COMSOL.
MR
Mads Jakob Herring Jensen
May 16, 2017Dear Marcel
We have no plans to extend the method to structural mechanics in the near future, but we are of course exploring the possibilities in a longer perspective.
Best regards
Mads
Yu Zhang
January 12, 2019Hi, Mads:
I am wondering which shape function type you choose to build this model, nodal discontinuous Lagrange or discontinuous Lagrange? I am trying to find the introduction about these two shape function types, but there is little content about them? Could you please provide the literature on which these two shape functions are defined?
Thank you for your time.
Yu
Mads Herring Jensen
January 15, 2019Hi Yu
When you use the Convected Wave Equation, Time Explicit physics interface we have per-selected correct shape functions and shape function order. The interface uses the “Nodal discontinuous Lagrange” elements. In the theory section for the Convected Wave Equation interface we have a few references to literature on the theory. For information about the elements, search the documentation for the section “Shape Function Types (Elements)” in the COMSOL Multiphysics Reference Manual.
Best regards,
Mads
Yu Zhang
January 15, 2019Hi, Mads:
Thank you for your valuble reply. I have read the help document, but still cannot find the introduction about the “discontinuous Lagrange”. Could you please provide some information or literature about it, or the difference between the “nodal discontinuous” and “discontinuous”?
Thank you for your help.
Mads Herring Jensen
January 21, 2019Hi Yu
You should be able to find details in one of the references that we state in the theory section for the Convected Wave Equation of the documentation. You can also search for the section “Theory for the Wave Form PDE” here you can also find a reference. But you are right, the difference is not clearly discussed in the doc, we will try to add that for the future. Thanks for the feedback!
Best regards
Mads
Magnus Ringh
January 23, 2019Hi Yu,
There is actually information about the discontinuous Lagrange and nodal discontinuous Lagrange elements in the COMSOL Multiphysics Programming Reference Manual, where they are referred to as the discontinuous elements shdisc and shhwdisc, respectively. The difference between them is that the latter (nodal discontinuous Lagrange) has optimal placement of the degrees of freedom on triangular and tetrahedral meshes with respect to certain interpolation error estimates, whereas the former (discontinuous Lagrange) is available on all types of mesh elements with arbitrary polynomial order.
For the next release, we will make the documentation more consistent regarding the names of these element types and add links to this information. Thanks again for your feedback!
Best regards,
Magnus Ringh, COMSOL