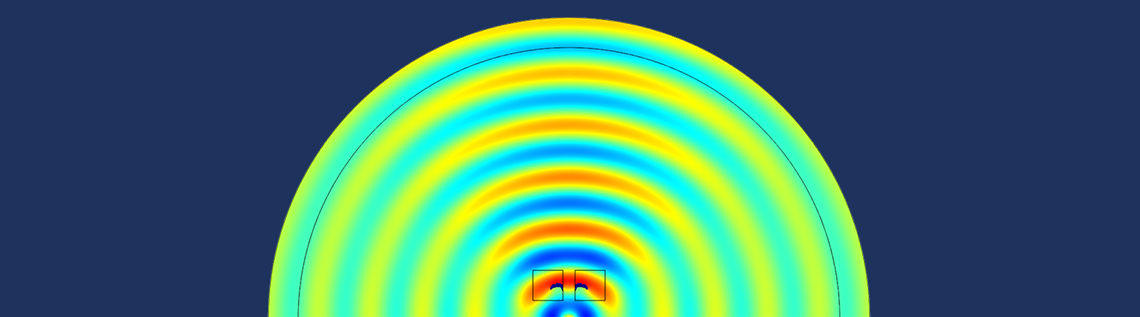
Today, guest blogger René Christensen of GN Hearing discusses the importance of acoustic topology optimization and how to apply it in COMSOL Multiphysics.
Topology optimization is a powerful tool that enables engineers to find optimal solutions to problems related to their applications. Here, we’ll take a closer look at topology optimization as it relates to acoustics and how we optimally distribute acoustic media to obtain a desired response. Several examples will further illustrate the potential of this optimization technique.
Objective Functions in Topology Optimization
Many engineering tasks revolve around optimizing an existing design or a future design for a certain application. Best practices and experiences derived from years of working within a given industry are of great importance when it comes to improving designs. However, optimization problems are often so complex that it is impossible to know if design iterations are pushing things in the right direction. This is where optimization as a mathematical discipline comes into play.
Before we proceed, let’s review some important terminology. In optimization — be it parameter optimization, shape optimization, or in our case topology optimization — there is always at least one so-called objective function. Typically, we want to minimize this function. For acoustic problems, we may want to minimize the sound pressure in a certain region, whereas for structural mechanics problems, we may want to minimize the stresses in a part of a structure. We state this objective as
with F being the objective function. A design variable \chi is varied throughout the optimization process to reach an optimal solution. It is varied within a design domain denoted Ωd, which generally does not make up the entire finite element space Ω, as visualized in the figure below.
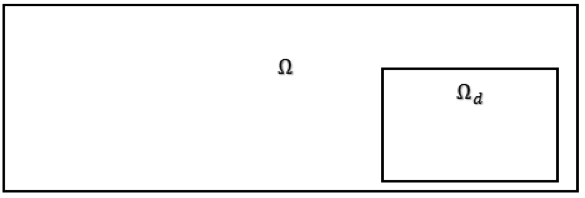
The design domain is generally a subset of the entire finite element domain.
Note that since the design variable varies as a function of space over the finite element discretized design domain, it is as such a vector. For this particular case, we will simply address it as a variable.
The optimization problem may have more than one objective function, and so it will be up to the engineer to decide how large of a weight each of these objectives should carry. Note that because the objectives may oppose each other during the optimization, special care should be taken when setting up the problem.
In addition to the objective function(s), there will usually be some constraints associated with the optimization problem. These constraints reflect some inherent size and/or weight limitations for the problem in question. With the Optimization interface in COMSOL Multiphysics, we can input the design variable, the objective function(s), and the constraints in a systematic way.
A Static Structural Mechanics Example
With topology optimization, we have an iterative process where the design variable is varied throughout the design domain. The design variable is continuous throughout the domain and takes on values from zero to one over the domain:
Ideally, we want the design variable to settle near values of either zero or one. In this way, we get a near discrete design, with two distinct (binary) states distributed over the design domain. The interpretation of these two states will depend on the physics related to our optimization. Since most literature addresses topology optimization within the context of structural mechanics, we will first look at this type of physics and address its acoustics counterpart in the next section.
Topology optimization in COMSOL Multiphysics for static structural mechanics was a previous topic of discussion on the COMSOL Blog. To give a brief overview: A so-called MBB beam is investigated with the objective of maximizing the stiffness by minimizing the total strain energy for a given load and boundary conditions. The design domain makes up the entire finite element domain. A constraint is applied to the total mass of the structure. In the design space, Young’s modulus is interpolated via the design variable \chi as
To help the binary design, we can use a so-called solid isotropic material with penalization (SIMP) interpolation
where p is the penalization factor, typically taking on a value in the range of three to five. With this interpolation (and an implicit linear interpolation of the density), intermediate values of X are avoided by the solver as they provide less favorable stiffness-to-weight ratios. I have recreated the resulting MBB beam topology from the previous blog post below.

Recreation of the optimized MBB beam.
In this figure, black indicates a material with a user-defined Young’s modulus of E0. Meanwhile, white corresponds to zero stiffness, indicating that there should be no material.
Performing Acoustic Topology Optimization in COMSOL Multiphysics®
Let’s now move on to our discussion of acoustic topology optimization, where we have a frequency-dependent solution with wave propagation in an acoustic media. The design variable is now related to the physics of acoustics. Instead of having a binary void-material distribution of material, our goal is to have a binary air-solid distribution, where “solid” refers to a fluid with a high density and bulk modulus, which emulates a solid structure.
We define four parameters that describe the inertial and compressional behavior of the standard medium and the “solid” medium: Air is given a density of \rho_1 and a bulk modulus of K1, and the “solid” medium has a higher density of \rho_2 and a higher bulk modulus of K2. The density \rho and bulk modulus K in the design domain will vary between the two states during the optimization via the design variable — similar to the variance of the Young’s modulus in our structural mechanics example. But a different interpolation is needed for an acoustics analysis so that the associated values do not tend to zero for a zero-valued design variable, but instead vary between air and the solid, so that
and
The easiest way to obtain these characteristics is by linear interpolation between the two extreme values. This is not necessarily the best approach since intermediate values of \chi will not be penalized and therefore the optimal design may not be binary. As such, it will not be feasible to manufacture. In the literature alternative, interpolation schemes are given. In the cases presented here, the so-called rational approximation of material properties (RAMP) interpolation is used (see Ref. 1).
Just as with structural optimization, we define a design domain where the material distribution can take place, while simultaneously satisfying the constraints. An area or volume constraints can be defined via the design variable. For example, an area constraint on the design domain can be stated as an inequality constraint
where Sr is an area ratio between the area of the design that is assigned solid properties and the entire design domain.
A Single-Objective, Single-Frequency Example
Let’s first take a look at a silencer (or “muffler”) example. For simplicity, we limit ourselves to a 2D domain. A typical measure used when characterizing a silencer is the so-called transmission loss, denoted TL, which is a measure of power input to power output:
The transmission loss is calculated using the so-called three-point method (see Ref. 2). We use this as our objective function, seeking to maximize it at a single frequency (in this case 420 Hz):
Two design domains are defined above and below a tubular section. The design domain is constrained in such a way that a maximum of 5% of the 2D area is the structure and thus 95% must be air:
The initial state for the design domain is 100% air, i.e., \chi = 0. The animation below shows the evolution from the initial state to the resulting topology.
An animation depicting the evolution from the initial state to the optimized silencer topology.
The optimized structure takes on a “double expansion chamber” (see Ref. 3) silencer topology. The transmission loss has increased by approximately 14 dB at the target frequency, as illustrated in the plot below. However, at all frequencies other than the target frequency, the transmission loss has also changed, which may be of great importance for the specific application. Therefore, a single-frequency optimization may not be the best choice for the typical design problem.
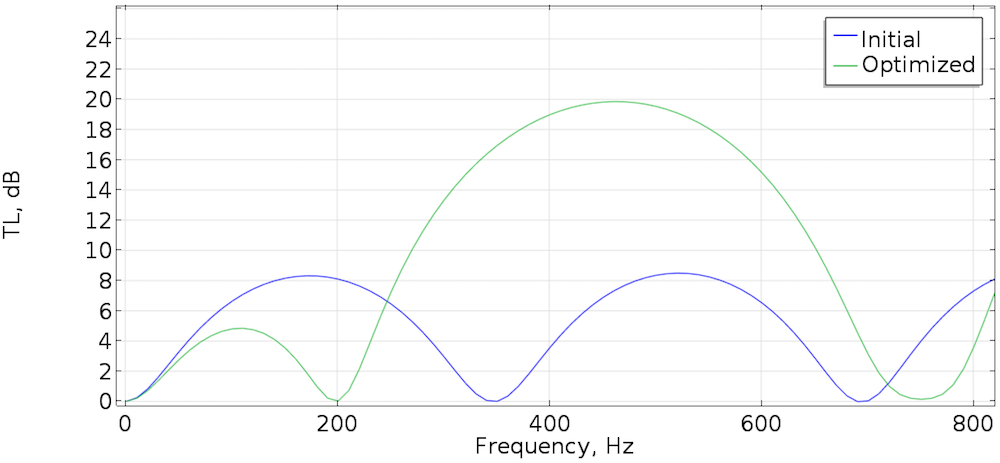
Transmission loss for the initial state and optimized silencer.
A Dual-Objective, Dual-Frequency Example
Shifting gears, let’s now look at how to optimize for two objective functions and two frequencies. Here, we again consider a 2D room with three hard walls and a pressure input at the left side of the room. The room also includes two objective areas, Ω1 and Ω2, defined at each corner at the right side of the room. The two objectives are as follows:
- Minimize the sound pressure level at a frequency f1 and
- Minimize the sound pressure level at a frequency f2 = 1.5 f1
with the circular design domain Ωd and an area constraint that is 10% structure. The initial state is \chi = 0, making the design domain 100% air.
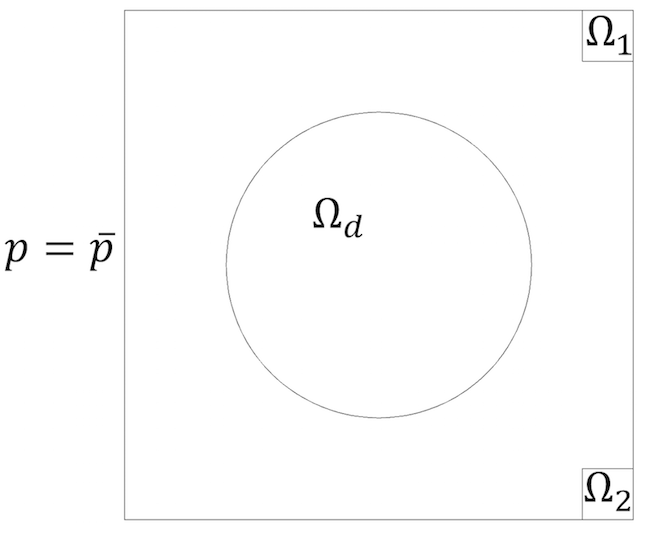
A square 2D room with a circular design domain and two objective domains.
With more than one objective function, we must make some choices regarding the relative weights, or importance, of the different objectives. In this case, the two objectives are of equal weight in importance, and the problem is stated as a so-called min-max problem:
\min_{\chi} \max_{f_1 f_2} SPL_i (\chi, f_i) \\
\text {subject to} \int^{}_{\Omega_d} \chi d\Omega_d \leq 0.1.
\end{align}
The figures below show the optimized topology (blue) along with the sound pressure for both frequencies using the same pressure scale. Note how the optimized topology results in a low-pressure zone (green) appearing in the upper-right corner at the first frequency. At the same time, this optimized topology ensures a similar low-pressure zone in the lower-right corner at the second frequency. This would certainly be a challenging task if trial-and-error was the only choice.
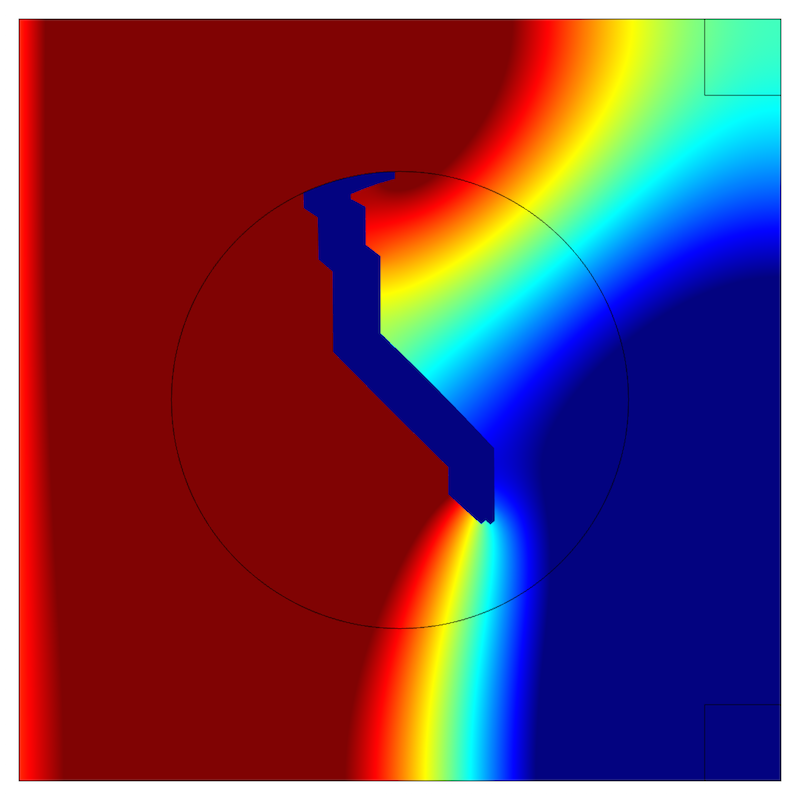
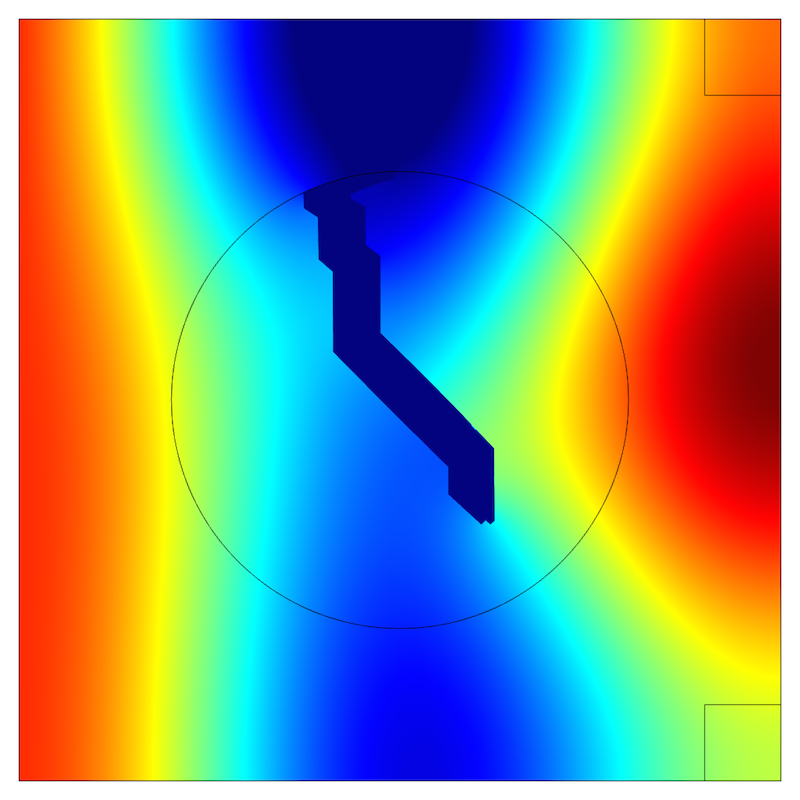
Sound pressure for frequency f1 (left) and for frequency f2 (right). The optimized topology is shown in blue.
A Single-Objective, Multiple Frequency Example
As a third and final example, we’ll optimize a single objective over a frequency range. A sound source is radiating into a 2D domain, where we initially have a cylindrical sound field. Two square design domains are present, but since there is symmetry, we only consider one half of the geometry in the simulation. In this case, we want a constant magnitude of the on-axis sound pressure of \overline{p}_{obj} in a point 0.4 meter in front of the sound source. The optimization is carried out in a frequency range of 4,000 to 4,200 Hz (50 Hz steps, a total of five frequencies). We can accomplish this via the Global Least-Squares Objective functionality in COMSOL Multiphysics, with the problem being stated as:
\min_{\chi} \sum_{i=1}^{5} (\mid p_i (\chi, f_i, 0, 0.4) \mid -\overline{p}_{obj})^2 \\
\text {subject to} \int^{}_{\Omega_d} \chi d\Omega_d \leq 0.1.
\end{align}
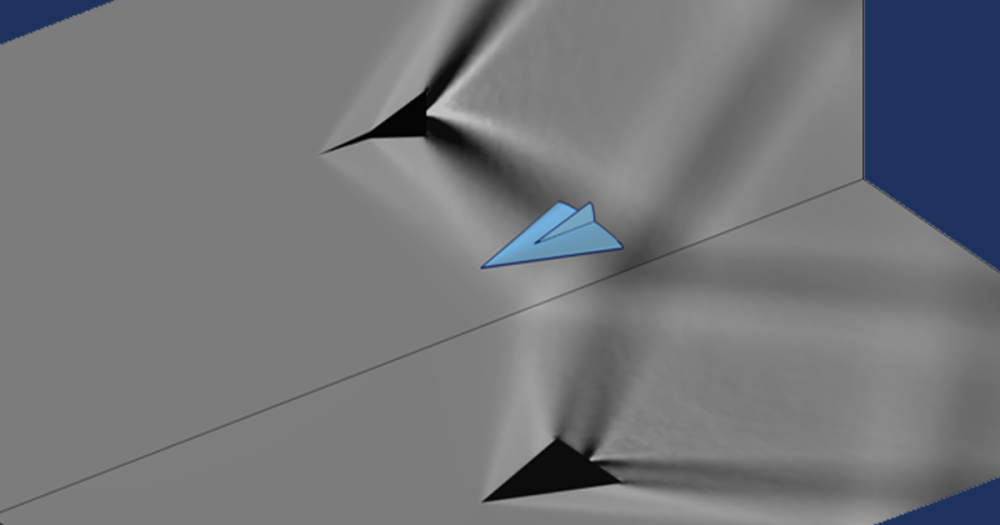
The initial state is again \chi=0. The optimized topology is shown below, along with the sound field for both the initial state and optimized state.
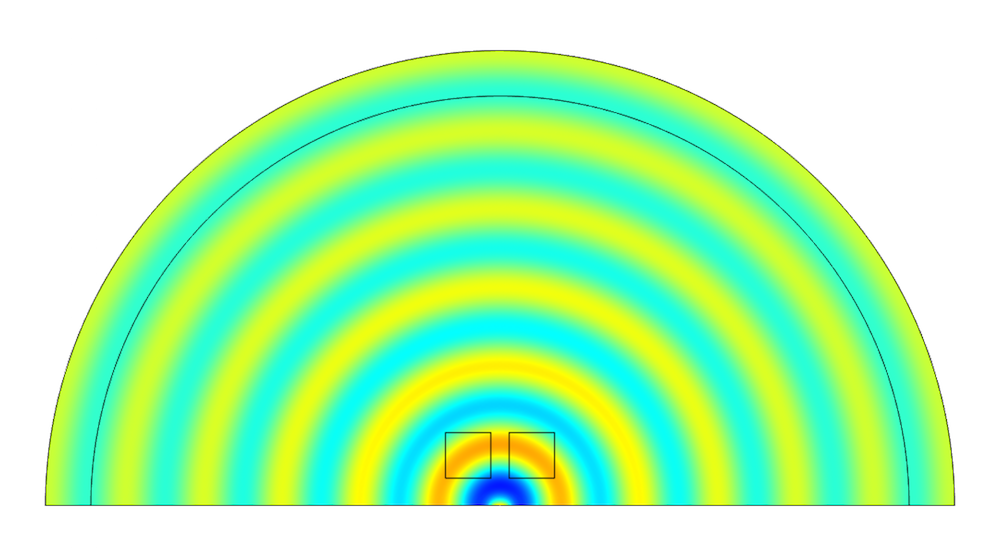
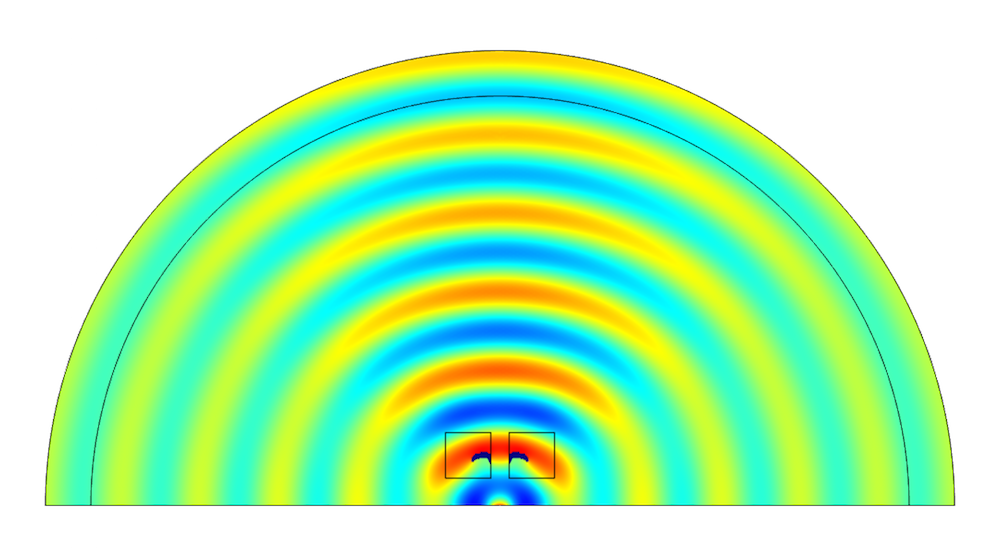
Sound pressure for the initial state (left) and optimized state (right) at 4 kHz, with the optimized topology shown in blue within the square design domains.
Since the sound pressure magnitude in the observation point of the initial state is lower than the objective pressure, the topology optimization results in the creation of a reflector that focuses the on-axis sound. The sound pressure magnitudes before and after the optimization are shown below. The pressure magnitude is close to the desired objective pressure in the frequency range following the optimization.
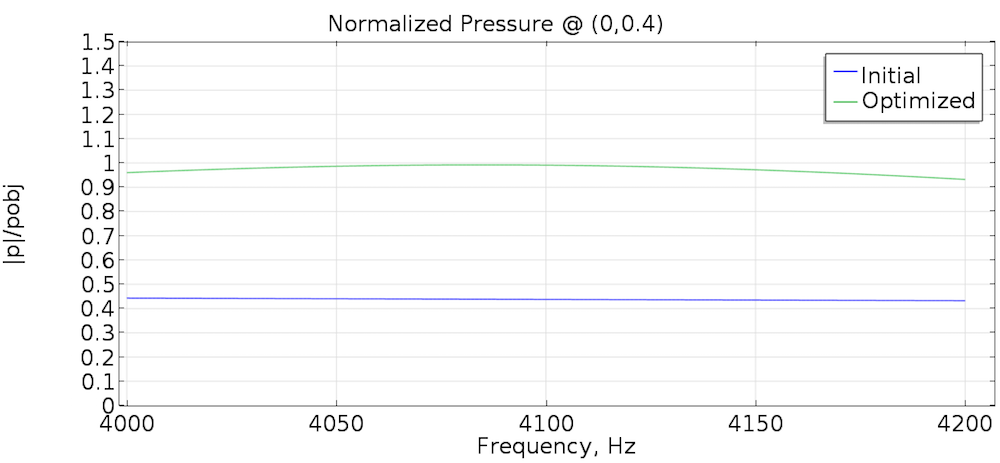
The pressure magnitude divided by \overline{p}_{obj} for the initial and optimized topology.
The Power of Acoustic Topology Optimization
Acoustic topology optimization offers great potential for helping acoustic engineers come up with innovative designs. As I have demonstrated today, you can effectively use this technique in COMSOL Multiphysics. With proper formulations of objectives and constraints, it is possible to construct applications with new and innovative topologies — topologies that would most likely not have been found using traditional methods.
I would like to give special thanks to Niels Aage, an associate professor at the Technical University of Denmark, for several fruitful discussions on the topic of optimization.
To learn more about using acoustic topology optimization in COMSOL Multiphysics, we encourage you to download the following example from our Application Gallery: Topology Optimization of Acoustic Modes in a 2D Room.
References
- M.P. Bendsoe, O. Sigmund, Topology Optimization: Theory, Methods, and Applications, Springer 2003.
- T.W. Wu, G.C. Wan, Muffler, “Performance studies and using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss”, Trans. ASME: J. Vib. Acoust. 118 (1996) 479-484.
- Z. Tao, A.F. Seybert, “A review of current techniques for measuring muffler transmission loss”, SAE International, 2003.
About the Guest Author
René Christensen has been working in the field of vibroacoustics for more than a decade, both as a consultant (iCapture ApS) and as an engineer in the hearing aid industry (Oticon A/S, GN Hearing A/S). He has a special interest in the modeling of viscothermal effects in microacoustics, which was also the topic of his PhD. René joined the hardware platform R&D acoustics team at GN Hearing as a senior acoustic engineer in 2015. In this role, he works with the design and optimization of hearing aids.





Comments (0)