A thorough analysis of a loudspeaker driver is not limited to a frequency-domain study. Some desirable and undesirable (but nonetheless exciting) effects can only be caught by a nonlinear time-domain study. Here, we will discuss how system nonlinearities affect the generated sound and how to use the COMSOL Multiphysics® software to perform a nonlinear distortion analysis of a loudspeaker driver.
Understanding Linear and Nonlinear Distortions
A transducer converts a signal of one energy form (input signal) to a signal of another energy form (output signal). In regard to a loudspeaker, which is an electroacoustic transducer, the input signal is the electric voltage that, in the case of a moving coil loudspeaker, drives its voice coil. The output signal is the acoustic pressure that the human ear perceives as a sound. A distortion occurs when the output signal quantitatively and/or qualitatively differs from the input signal.
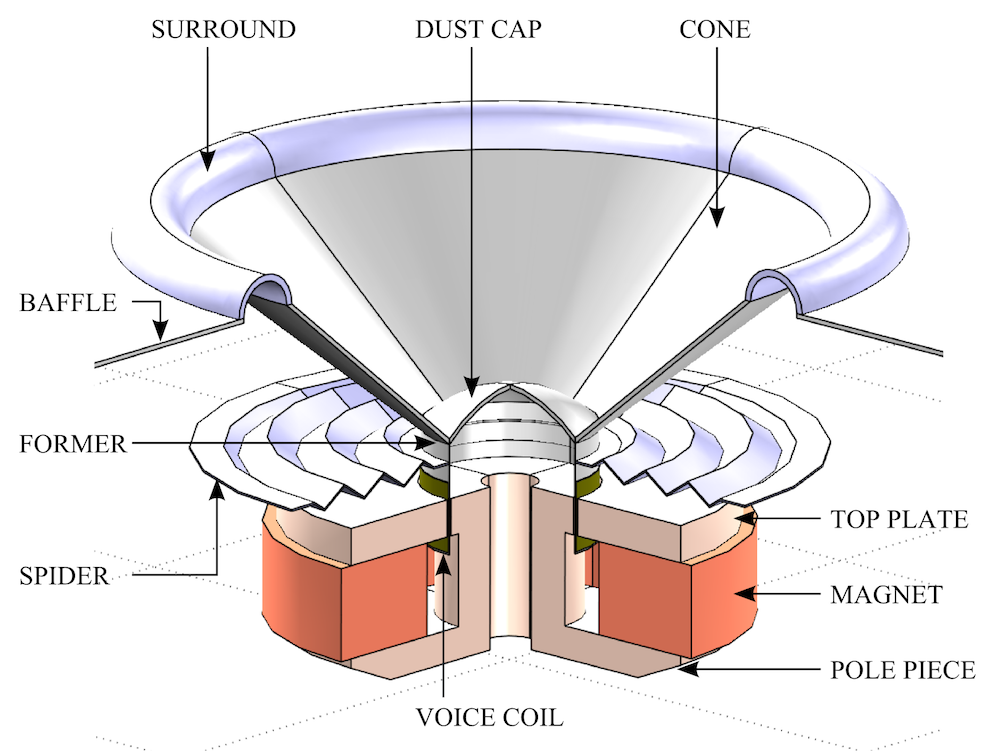
Schematic representation of a moving coil loudspeaker.
The distortion can be divided into two principal parts:
- Linear distortion
- Nonlinear distortion
The term linear distortion, which might sound rather confusing, implies that the output signal has the same frequency content as the input signal. In this distortion, it is the amplitude and/or phase of the output signal that is distorted. In contrast, the term nonlinear distortion suggests that the output signal contains frequency components that are absent in the input signal. This means that the energy is transferred from one frequency at the input to several frequencies at the output.
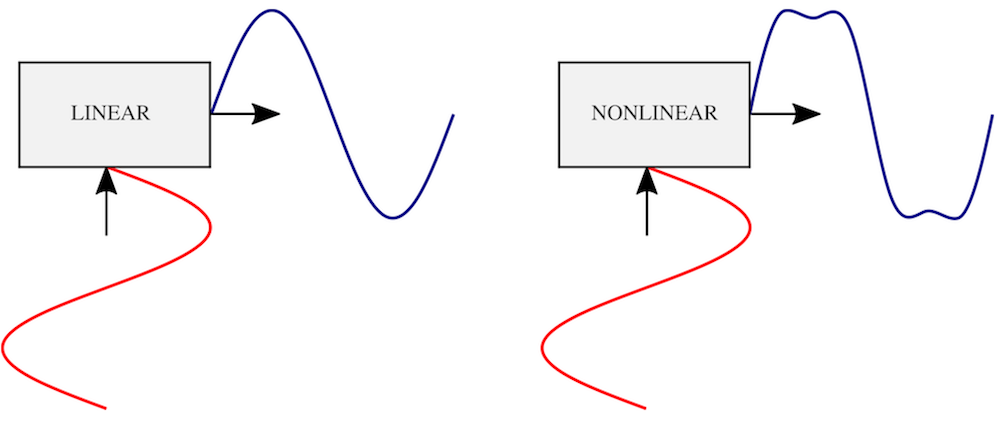
Input and output signals in linear and nonlinear transducers.
Let the input sinusoidal signal, A_\text{in} \sin \left( 2\pi f t \right), be applied to a transducer with a nonlinear transfer function. The frequency content of the output signal will then have more than one frequency. Apart from the fundamental portion, which corresponds to the frequency f, there will be a distorted portion. Its spectrum usually (but not always) consists of the frequencies f^{(2)}, f^{(3)}, f^{(4)}, \ldots, which are multiples of the fundamental frequency f^{(n)} = n f, in which n \geq 2. These frequencies, called overtones, are present in the sound, and it is the overtones that make musical instruments sound different: A note played on a violin sounds different from the same note played on a guitar. The same happens with the sound emitted from a loudspeaker.
The distortion is a relative quantity that can be described by the value of the total harmonic distortion (THD). This value is calculated as the ratio of the amplitude of the distorted portion of the signal to that of the fundamental part:
The profile of a signal with a higher THD visibly differs from the pure sinusoidal.
Unfortunately, the value of the THD of the output signal itself might not be enough to judge the quality of the loudspeaker. A signal with a lower THD may sound worse than a signal with a higher THD. The reason is that the human ear perceives various overtones differently.
The distortion can be represented as a set of individual even-order, 2nf, and odd-order,
(2n-1)f, components. The former are due to asymmetric nonlinearities of the transducer, while the latter are due to symmetric nonlinearities. The thing is that the sound containing even-order harmonics is perceived as “sweet” and “warm”. This can be explained by the fact that there are octave multiples of the fundamental frequency among them. The odd-order harmonics sound “harsh” and “gritty”. That is quite alright for a guitar distortion pedal, but not for a loudspeaker. What matters is, of course, not just the presence of those harmonics, but rather their level in the output signal.
Another interesting effect, called intermodulation, occurs when the input signal contains more than one frequency component. The corresponding output signals start to interact with each other, producing frequency components absent in the input signal. In practice, if a two-tone sine wave such as A_\text{in} \sin \left( 2\pi f_1 t \right) + B_\text{in} \sin \left( 2\pi f_2 t \right) (in which f_2 > f_1) is applied to the input, the system nonlinearities will result in the modulation of the higher-frequency component by the lower one. That is, the frequencies f_2 \pm f_1, f_2 \pm 2f_1, and so on will appear in the frequency spectrum of the output signal. The quantitative measure of the intermodulation that corresponds to the frequency, f_2 \pm (n-1) f in which n \geq 2, is the nth-order intermodulation distortion (IMD) coefficient. It is defined as:
In practice, using an input signal containing three or more frequencies for the IMD analysis is not advisable, as the results become harder to interpret.
Transient Nonlinear Analysis of a Loudspeaker Driver
To summarize, the linear analysis of the loudspeaker, though a powerful tool for a designer, might not be sufficient. The loudspeaker can only be completely described if an additional nonlinear analysis is carried out. The nonlinear analysis is supposed to answer the following questions:
- How does the nonlinear behavior of the loudspeaker affect the output signal?
- What are the limits of the input signal that ensure the loudspeaker functions acceptably?
- How should I compensate for the undesired distortion of the loudspeaker?
From the simulation point of view, there is both bad and good news. The bad news is that the full nonlinear analysis cannot be performed in the frequency domain. It requires the transient simulation of the loudspeaker, which is more demanding and time consuming than the frequency-domain analysis. The good news is that the effect of certain nonlinearities is only significant at low frequencies.
For example, the voice coil displacement is greater at lower frequencies and therefore the finite strain theory must be used to model the mechanical parts of the motor. Using the finite strain theory is redundant at higher frequencies, where the infinitesimal strain theory is applicable. The figures below show the results for the transient loudspeaker tutorial, driven by the same amplitude (V_0 = 10 V) of input voltage:
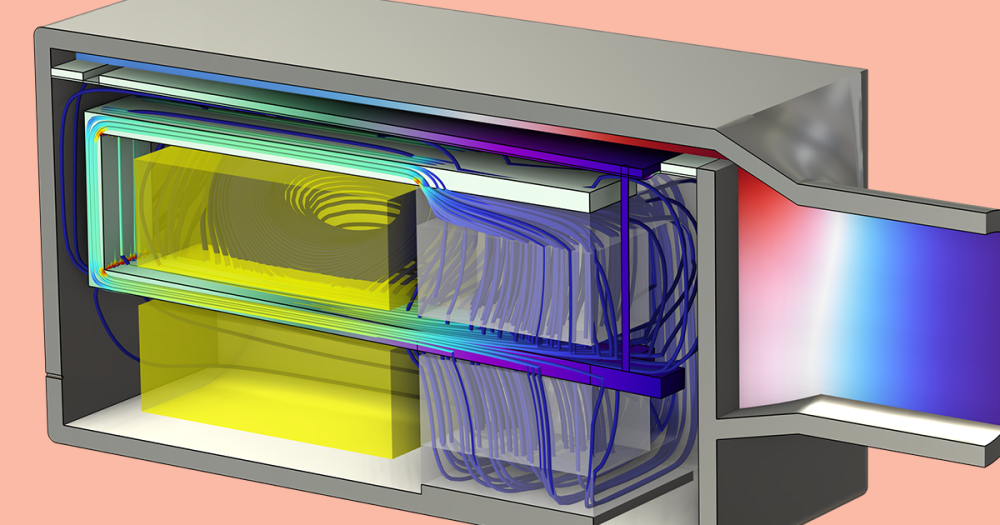
Voice coil motion in the air gap of the loudspeaker driver for a single-tone input voltage signal: 70 Hz on the left and 140 Hz on the right.
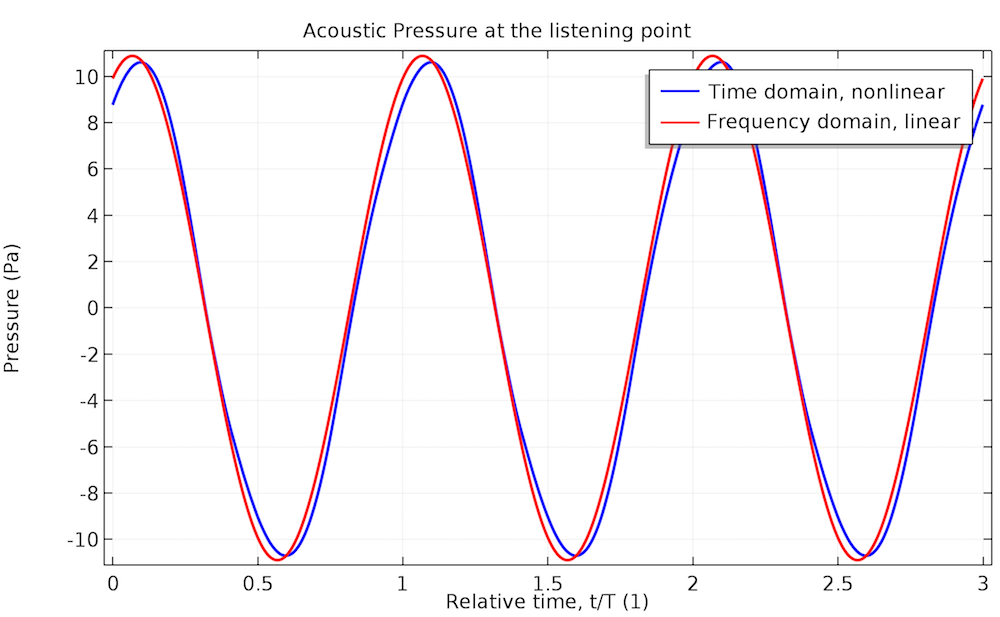
Acoustic pressure at the listening point for a single-tone input voltage. The blue curves correspond to the nonlinear time-domain analysis, while the red curves correspond to the frequency-domain analysis: 70 Hz on the left and 140 Hz on the right.
The animations above depict the magnetic field in the voice coil gap and the motion of the former and the spider (both in pink) as well as the voice coil (in orange). As expected, the displacements, as well as the spider deformation, are higher at the lower frequency. The spider deformation obeys the geometrically nonlinear analysis and therefore the linear approximation is inaccurate in this case. This is confirmed by the output signal plots. These plots depict the acoustic pressure at the listening point located about 14.5 cm in front of the speaker dust cap tip.
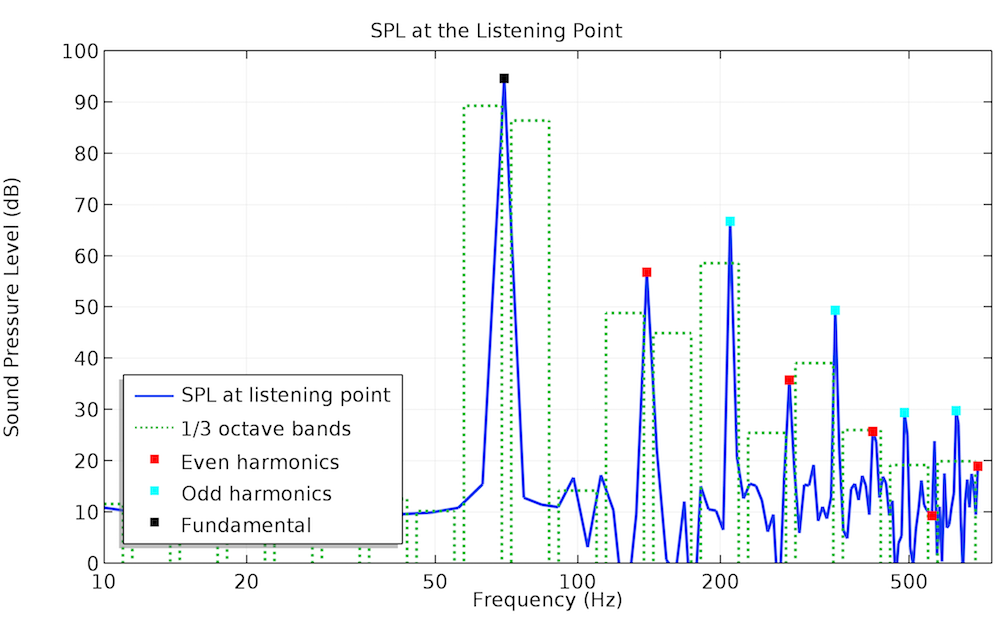
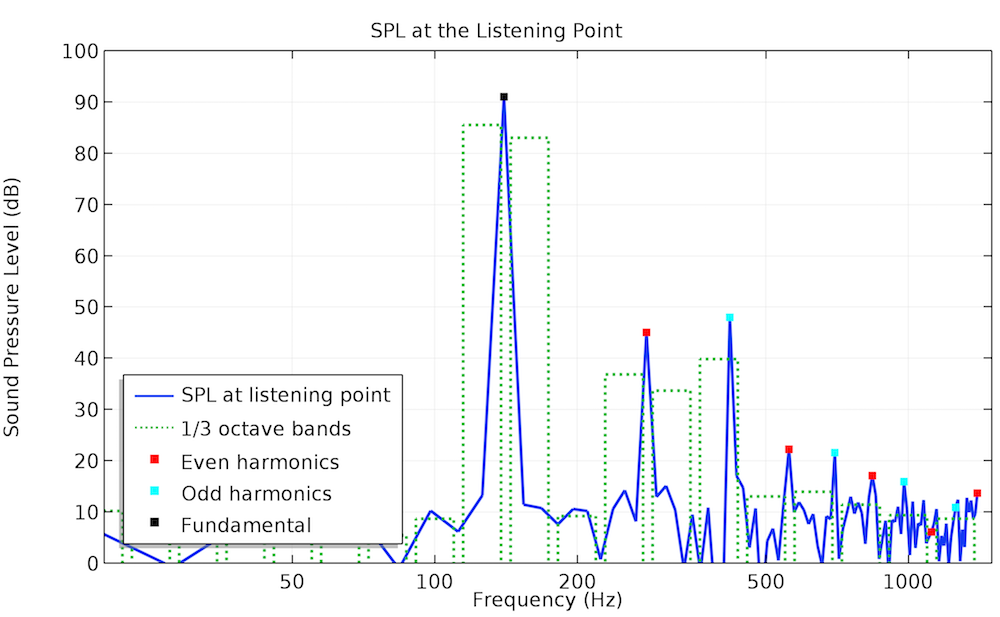
The acoustic pressure profile obtained from the nonlinear time-domain modeling for the 70-Hz input signal deviates from the sinusoidal shape to a certain extent, which means that higher-order harmonics start playing a definite role. This is not visible for the input signal at 140 Hz: There’s only a slight difference in the amplitude between the linear frequency-domain and nonlinear time-domain simulation results. The THD value of the output signal drops from 4.3% in the first case to 0.9% in the second case. The plots below show how the harmonics contribute to the sound pressure level (SPL) at the listening point.
Frequency spectra of the SPL at the listening point: single-tone input voltage (70 Hz on the left and 140 Hz on the right).
The IMD analysis of the loudspeaker is carried out in a similar way. What’s different is the input signal applied to the voice coil, which contains two harmonics parts:
whose amplitudes, V_1 and V_2, usually correlate as 4 : 1, which corresponds to 12 dB.
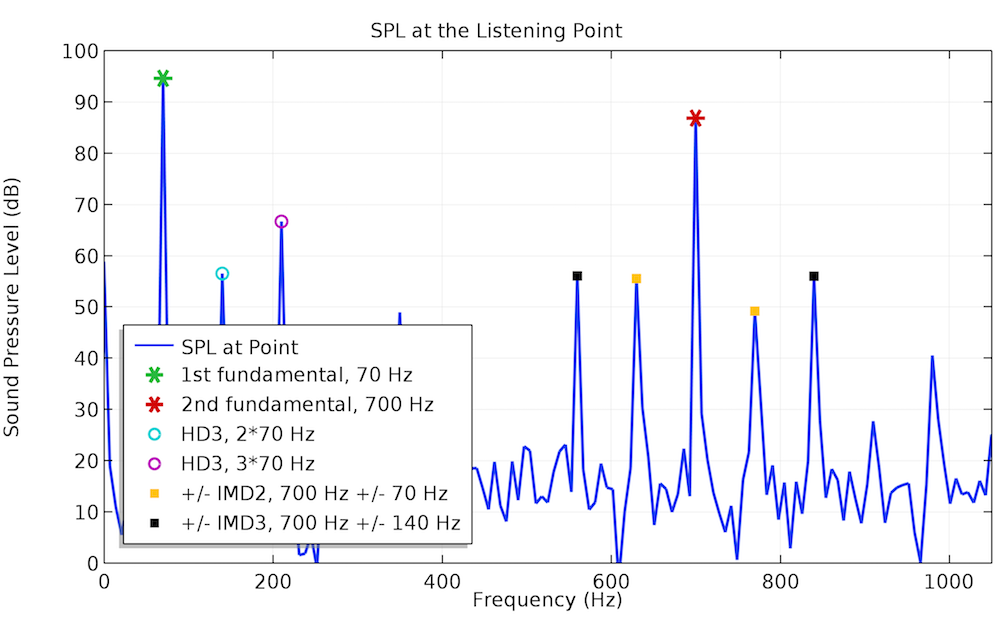
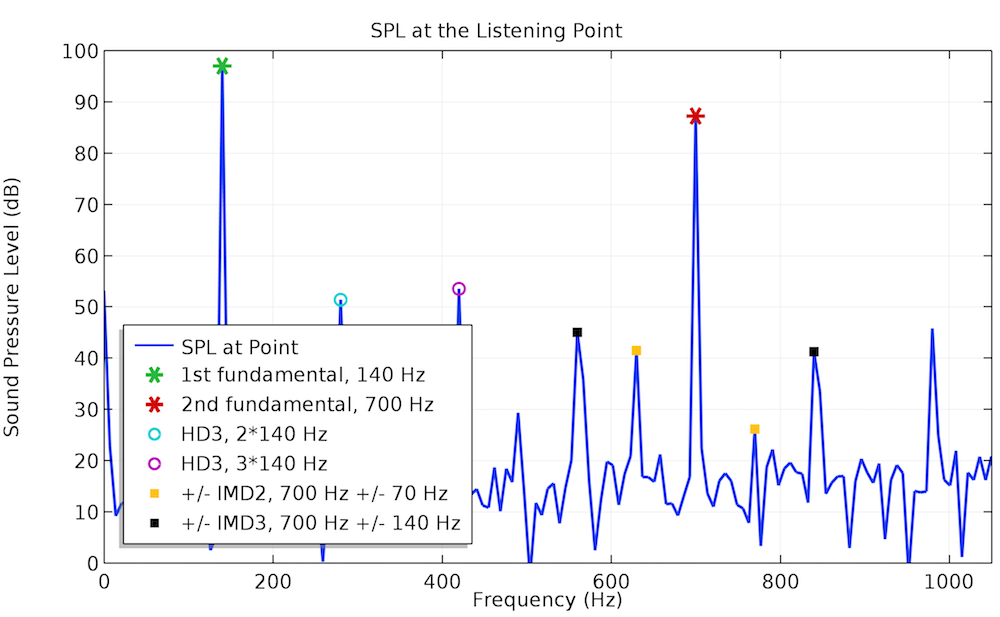
The example below studies the IMD of the same test loudspeaker driver. The dual-frequency input voltage, in which f_1 = 70 Hz and f_2 = 700 Hz, serves as the input signal. The SPL plot on the left shows how the second- and third-order harmonics arising in the low-frequency part of the output signal generate a considerable level of the corresponding order IMDs in the high-frequency part. The IMD level becomes sufficiently lower if the signal frequency f_1 is increased to 140 Hz. This is seen in the right plot below.
Frequency spectra of the SPL at the listening point for a two-tone input voltage.
Modeling Tips for Analyzing a Loudspeaker Driver
Since transient nonlinear simulations tend to be demanding, the loudspeaker driver model should not be overcomplicated. The 2D axisymmetric formulation is a good starting approach and was used for the tutorial examples in the previous section. After that, it’s important to estimate which effects are more important than others. This will help you set up an adequate multiphysics model of a loudspeaker.
The system nonlinearities include, but are not limited to, the following:
- Nonlinear behavior of the magnetic field in the loudspeaker pole piece made of high-permeability metal
- Geometric nonlinearities in the moving parts of the motor
- Topology change as the voice coil moves up and down in the air gap
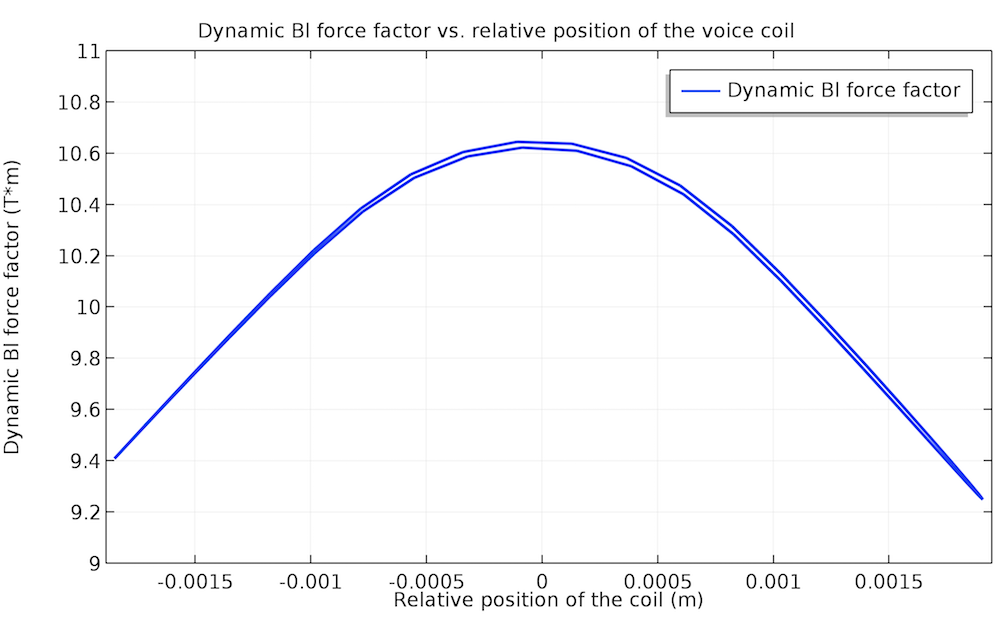
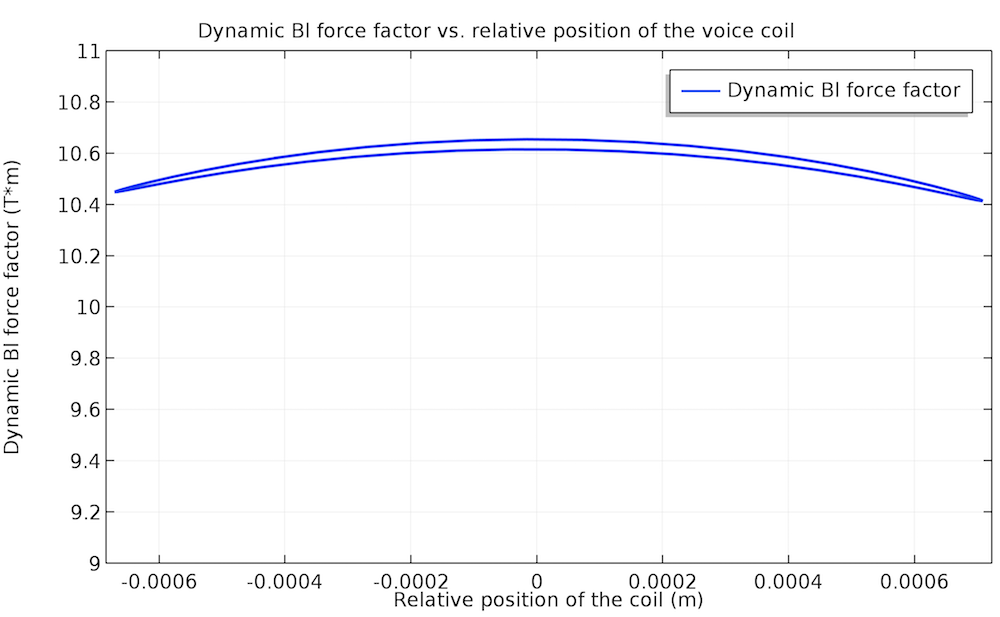
Speaking the lumped parameters’ language, this means that they are no longer constants like the Thiele-Small parameters, but functions of the voice coil position, x, and the input voltage, V. The above-mentioned nonlinearities will be reflected in the nonlinear inductance, L \left( x, V \right); compliance, C \left( x, V \right); and dynamic force factor, Bl \left( x, V \right). For instance, the tutorial example shows that the nonlinear behavior of the force factor is more distinct at 70 Hz, whereas it is almost flat (that is, closer to linear) at 140 Hz.
Nonlinear (left) and almost linear (right) behavior of the dynamic force factor: 70 Hz on the left and 140 Hz on the right.
With the following steps, the discussed nonlinearities can be incorporated into the model. First, the nonlinear magnetic effects are taken into account through the constitutive relation for the corresponding material. In the test example, the BH curve option is chosen for the iron pole piece. Next, the Include geometric nonlinearity option available under the Study Settings section forces the structural parts of the model to obey the finite strain theory. Lastly, the topology change is captured by the Moving Mesh feature. Whenever applied, the feature ensures that the mesh element nodes move together with the moving parts of the system. Since the displacements can be quite high, it is likely that the mesh element distortion reaches extreme levels and the numerical model becomes unstable. The Automatic Remeshing option is used as a remedy against highly distorted mesh elements.
All in all, the nonlinear time-domain analysis of the loudspeaker requires much more effort and patience than the linear frequency-domain study. This is especially relevant when the model includes the Moving Mesh feature with the Automatic Remeshing option activated. Investing some time in the geometry and mesh preprocessing will pay off, as the moving mesh is very sensitive to the mesh quality. That is, highly distorted mesh elements and near-zero angles between the geometric entities have to be avoided. A proper choice of the Condition for Remeshing option may also require some trial and error.
The loudspeaker design discussed here might not be considered “good” by most standards. The odd-order harmonics prevail in the frequency content of the output signal.
Next Steps
To perform your own nonlinear distortion analysis of a loudspeaker, click on the button below. This will take you to the Application Gallery, where you can find the MPH-files for this model together with detailed modeling instructions.
Additional Resources
- Check out other examples of modeling loudspeakers in these tutorials:
- Further reading:
- L.L. Beranek and T.J. Mellow, Acoustics: Sound Fields and Transducers, Academic Press, 2012.
- Brüel & Kjær, “Audio Distortion Measurements,” Application Note BO0385, 1993.
- W. Marshall Leach, Jr., Introduction to Electroacoustics and Audio Amplifier Design, Kendall Hunt, 2010.






Comments (5)
Andri Bezzola
June 18, 2018Cool stuff, how long does your solution take to determine thd or imd? I tried something similar two years back for an AES paper, and we wanted 44.1khz resolution to measure full distortion. We included the structural mechanics part as a nonlinear ODE with values measured with a Klippel analyzer. But we also remeshed at every step and I wonder if the automatic remesh would make the simulation run faster. http://www.aes.org/events/141/papers/?ID=5026
Julian Lu
October 15, 2018Can COMSOL compute the spectrum of THD & IMD for loudspeaker at the listening point? Which module of COMSOL process the digital signal input to speaker model?
Kirill Shaposhnikov
October 17, 2018Dear Julian,
Could you please clarify the meaning of the “spectrum of THD & MHD” for me? Both THD and MHD are just numbers – constants – for an input signal of a certain frequency, f.
The input signal in this model is a voltage applied to the voice coil, that is Vin(t) = V0*sin(2*pi*f*t).
Julian Lu
May 23, 2019Dear Kirill.
Come back again since searching COMSOL capability for speaker. For each one of fundamental frequency, you can get the THD from several harmonics computation. However, I want to know whether COMSOL can compute the whole frequency band between 100Hz~20kHz. That means the THD spectrum. About the meaning of IMD, its full name is “InterModulation Distortion”. It’s some kind of nonlinear distortion, just the formula above this article. I want to know whether there is any spectrum chart showing THD & IMD.
Xiuyuan Peng
April 2, 2024Is there a specific reason we want to use a sine wave for excitation? Can we use an exponential sweep just like what we do in real measurements so that both the FR and THD can be derived for all frequencies? I believe this approach is especially suited for simulation as we don’t suffer from SNR problems.