
While designing a structure, have you ever been unsure of how to achieve the best shape? If so, then you will want to add a useful technique called shape optimization to your COMSOL Multiphysics modeling skill set. Today, we will discuss the concept of shape optimization and demonstrate its use through a classical problem.
A Background on Shape Optimization
As engineers, researchers, and scientists, we are always striving to come up with improved designs. Optimization is the idea of altering model inputs, such as part dimensions and material properties, with the objective of improving some metric, while also considering a set of constraints. The Optimization Module in COMSOL Multiphysics is a useful tool for addressing such problems.
Dimensional optimization is one of the more common optimization techniques. The approach involves changing CAD dimensions directly to minimize mass, as illustrated in our Multistudy Optimization of a Bracket tutorial. In the bracket example, we use so-called gradient-free techniques to adjust dimensions and consider constraints on the relationships between the dimensions, the peak stress, and the lowest natural eigenfrequency. These techniques are very flexible in the type of objective functions and constraints that can be addressed. However, one drawback to these techniques is having to remesh the part repeatedly to numerically approximate the sensitivities of the objective function and constraints with respect to the design variables.
As we have previously discussed on the blog, it is also possible to analytically compute the design sensitivities due to geometric changes when using the Deformed Geometry interface. Further, the gradient-based solvers can use the sensitivities to optimize the dimensions of a part without remeshing — an element that we highlighted in the design of a capacitor. It is helpful to review the two blog posts referenced here to understand the functionality that we will use today.
Shape optimization is an extension of the previously developed concepts, and it considers not just straightforward dimensional changes, but general changes in shape as well. The shape of the structure is controlled via a set of design parameters that use a set of basis functions, which can describe quite arbitrary shapes. Let’s take a look at an example.
Shape Optimization Problem: The Thickness of a Beam
We begin with a classical shape optimization problem: adjusting the thickness of a cantilevered beam to minimize the mass, while maintaining a constraint on the peak deflection of the free end. The beam of initially uniform thickness has a nonuniform load distributed over its top surface, as shown in the diagram below.
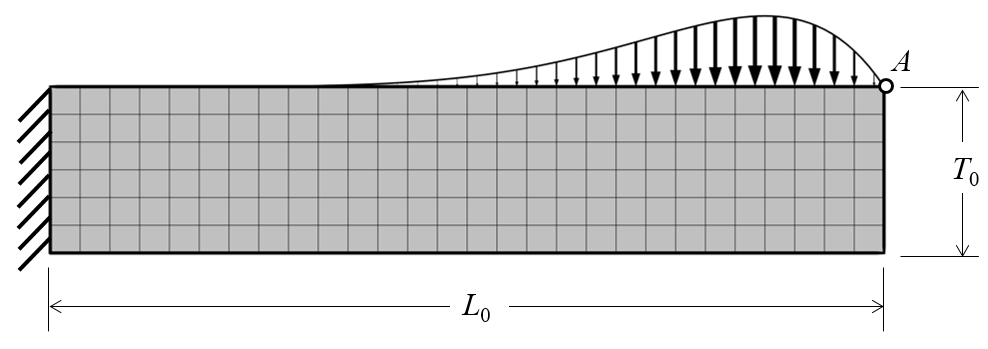
A cantilevered beam with a nonuniform load applied. Point A should not deflect more than a specified value. The mesh is also shown.
First, we want to choose our design variables. Both the length of the beam and the thickness at the cantilevered end are fixed. What we can vary is the thickness of the beam along the length. It is somewhat simpler to vary the change in the thickness from the initial configuration. Instead, we introduce a function, DT(X), which is initially zero along the length.
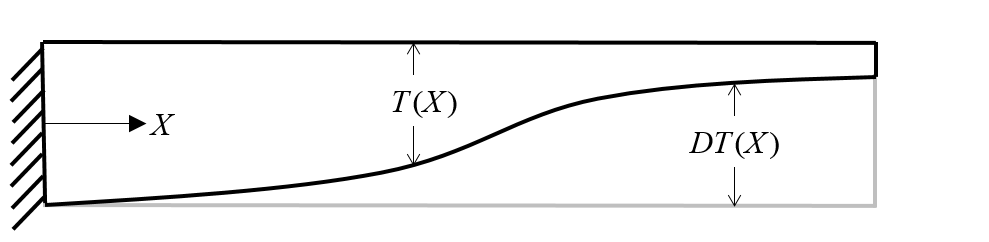
The optimization problem studies a change in the thickness of the beam.
Here, we choose to represent the change in thickness via a set of Bernstein polynomials of the fourth order:
expressed in terms of the normalized dimension: \bar X = X/L_0. Note that the function is scaled such that the polynomial coefficients have an order of magnitude near unity. Again, we do this for scaling purposes.
Since the thickness of the beam at X=0 is specified, DT(\bar X)=0, fixing C_0=0 so that the term can be omitted. At the far end, we add the constraint that the beam cannot become too thin: C_4<0.9.
In the intermediate region, we would also like to add some constraints to further limit the design space. We could add the constraint that 0 < DT(\bar X) < 0.9T0. The constraint, however, has a drawback: It would allow the thickness of the beam to oscillate and, from first principles, we know that this is not reasonable. There is no advantage to having the thickness of the beam increase along the length. We can instead add a constraint on the derivative: DT^\prime(\bar X) > 0. This forces the thickness of the beam to change monotonically along the length and has the added advantage of naturally satisfying the constraint: 0 < DT(\bar X) < 0.9T0.
There is one more constraint to consider: the displacement of the point at the end of the beam. We want the magnitude of the displacement of point A to be less than some specified value, u_{max}. With such information, we now have a complete optimization problem:
Here, the normalization of the objective function with respect to the initial mass of the beam, M_0, is done to scale the objective function so that it is of order unity. Similarly, the magnitude of the displacement of the beam tip, |\mathbf{u}_A|, is normalized with respect to the peak permissible displacement, u_{max}. The normalized displacement should be less than one. Let’s now look at implementing such a problem in COMSOL Multiphysics using the Optimization Module.
Implementing the Problem in COMSOL Multiphysics
We can begin with our initial design, simply a beam of fixed length and uniform thickness. The design is cantilevered at one end, with a nonuniform load across the top face that varies as \bar X^4(1-\bar X ). We want to first introduce the change in the thickness function. The polynomial function described earlier is the variable DT, as shown in the screenshot below. The expression Xg refers to the x-dimension of the original, undeformed geometry. The derivative of this function, with respect to the normalized x-direction, is the variable dDTdX. Two Global Parameters, L0 and T0, define the length and maximum thickness.
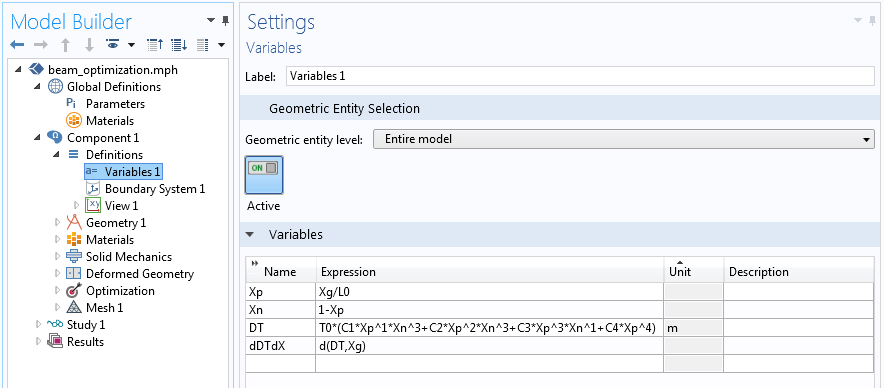
A screenshot showing the change in the thickness function and its derivative.
The change in the thickness variable is used within the Deformed Geometry interface to define how the entire volume of the beam is altered with a change in thickness. Since it is only the thickness that changes, a simple linear mapping can be used, as illustrated below.
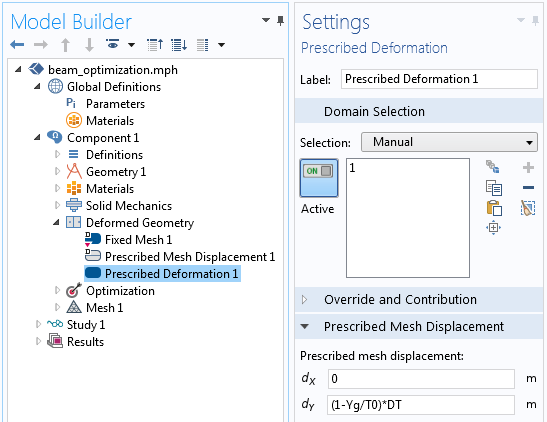
The displacement within the beam is completely prescribed.
We can now set up the optimization problem via the Optimization interface. The interface provides an easy way of setting up more complicated optimization problems with several constraints. The relevant settings are shown in the screenshots below, starting with the objective function. The Integral Objective feature integrates the material density over the modeling domain and normalizes with respect to the initial part mass.
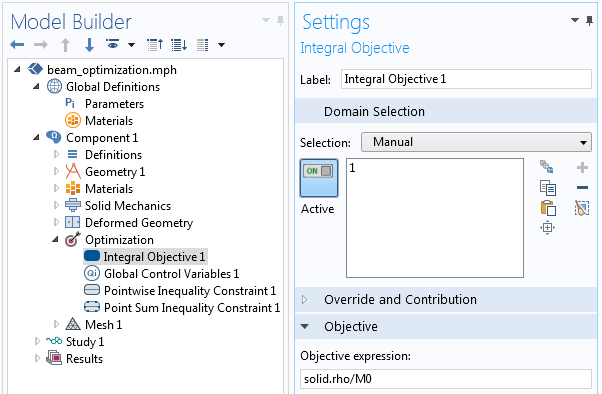
The optimization objective is to minimize the mass.
The settings for the Global Control Variables feature are shown below. The four variables, C1, C2, C3, and C4, have an initial value of zero, which is equivalent to the initial beam shape. The constraint on C4 is imposed as an upper bound and the scaling of all variables is unity.
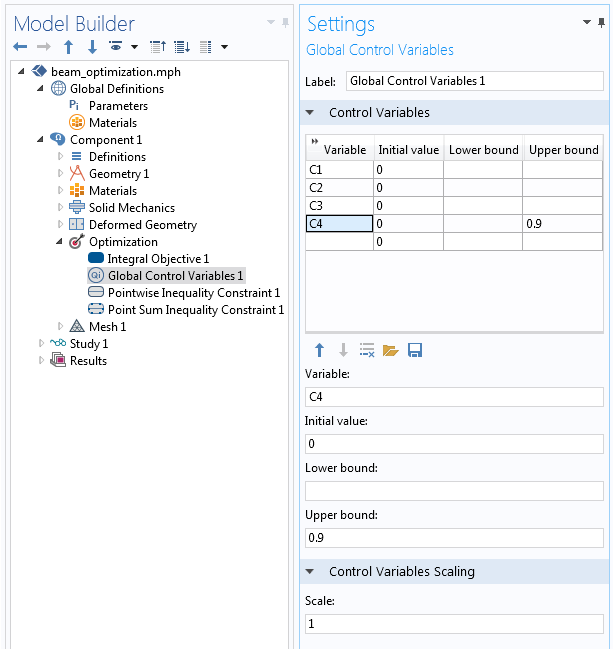
The definitions of the control variables, their bounds, and scaling.
Next, we apply the Pointwise Inequality Constraint feature to the bottom boundary of the domain. This feature enforces that the derivative of the displacement function remains positive at every point, thereby ensuring a monotonically increasing function.
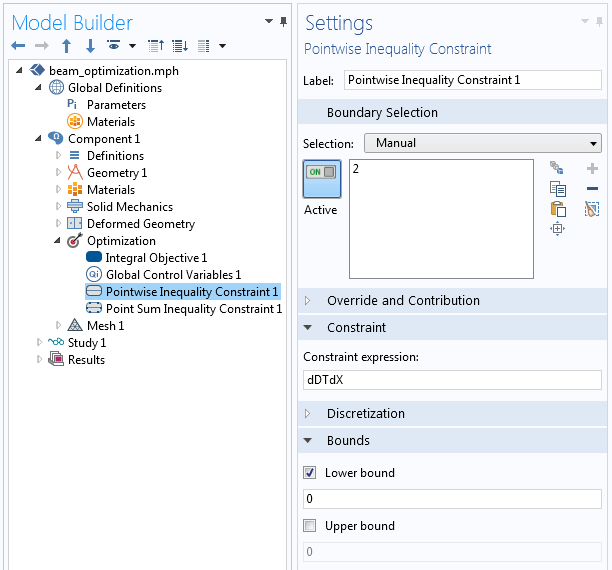
The constraint on the derivative along the length of the beam is enforced via a pointwise inequality constraint.
Finally, the peak displacement of the point at the far end of the beam is constrained so that it is below a maximum specified value. This value is set via the Point Sum Inequality Constraint feature.
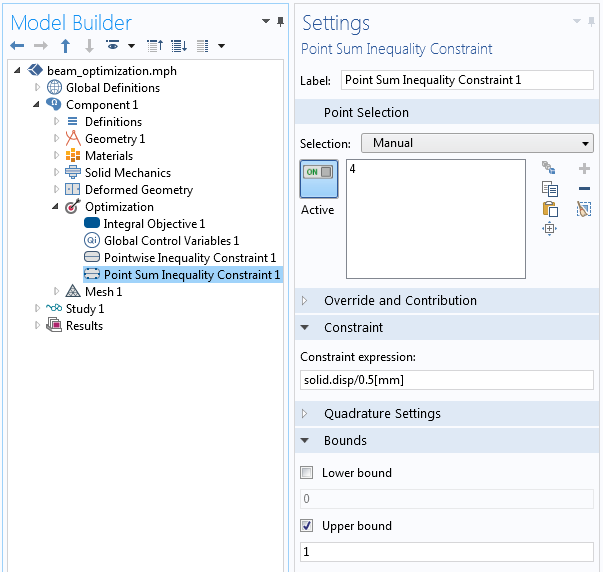
The implementation of the constraint on the normalized peak displacement.
Our optimization problem is now almost entirely set up. The only remaining step is to add an Optimization feature to the study sequence and to select the gradient-based SNOPT solver, which proves to be the fastest approach to our problem. All other settings can be left at their default values. The objective function and constraints are automatically taken from the Optimization interface.
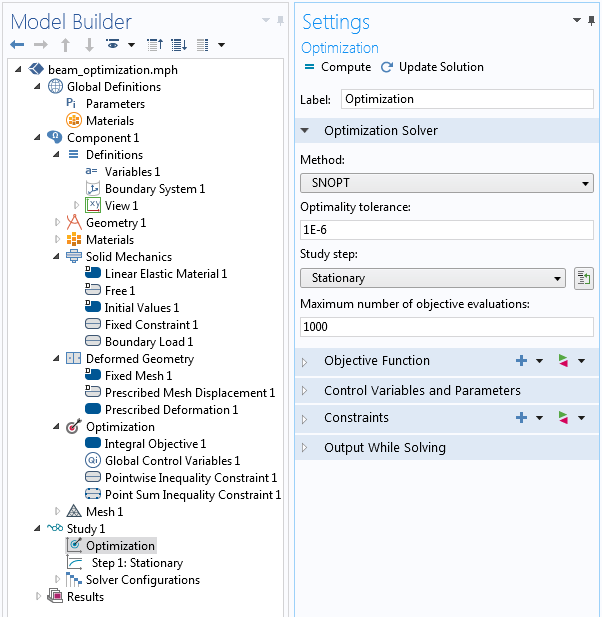
The relevant optimization solver settings.
The results are depicted in the image below. The optimal shape within this basis has been identified. The displacement at the tip is at its maximum value, with the thickness monotonically changing along the length. Due to the expected deformation of the geometry, a mapped mesh was used.
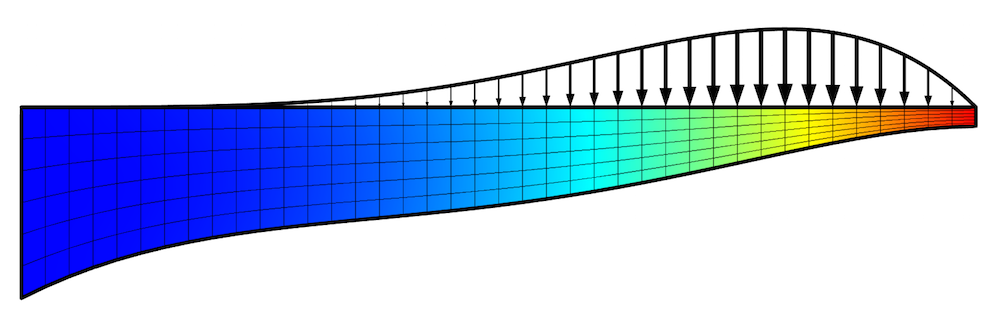
The optimized shape of the beam, which minimizes mass for the applied nonuniform load and constraints. The displacement field is plotted along with the applied load distribution and the mesh.
Summary of Using Shape Optimization to Design New Structures
We may ask ourselves how we know that the above structure is truly optimized. There is always the urge to perform a mesh refinement study, trying out finer and finer meshes to see how the solution converges. It is also reasonable to study convergence with respect to basis functions. We can use a higher-order Bernstein basis function and compare the results. This, however, can lead to a problem known as Runge’s phenomenon, along with slow convergence.
We can circumvent such issues by subdividing the original interval into multiple subintervals, using different lower-order shape functions within each interval (a piecewise polynomial). Other basis functions beyond the Bernstein basis can also be applied, such as the Chebyshev polynomials and the Fourier basis. The Optimizing the Shape of a Horn tutorial, available in our Application Gallery, features an example of the latter instance.
The cases discussed here include quite simple deformations. When considering more complicated deformations, you will need to put more effort into defining the deformation mapping. For very complicated deformations, it is also useful to add helper equations in order to compute the deformation.
If you have any questions about using these shape optimization techniques or are interested in adding the Optimization Module to your suite of modeling tools, please contact us.





Comments (6)
Matheus Magalhães
May 6, 2019Hello!
What should I do if I want to fix the 4 corners of the beam ?
Felipe Beltran-Mejia
May 9, 2019Hi Walter,
Thanks for the great post.
I still don’t get why by defining the prescribed mesh displacement as dy=(1-Yg/T0)*DT , the lower boundary gets deformed while the upper boundary stays the same. I dont see where in this equation this is implicit.
Best.
Vishal Dolas
August 2, 2021Hello, Why the exact same optimization does not work in 3D?
Walter Frei
August 2, 2021 COMSOL EmployeeThe same approach will work in 3D, but it will be a bit more steps to set up.
Song Han
February 26, 2022Hello Walter,
Could you share exactly the same model same as the workflow given in this blog. I know that the advanced version of COMSOL (5.6 or 6.0) has the “beam_optimization.mph” but the workflow seems different from the screenshots in this blog.
Walter Frei
February 28, 2022 COMSOL EmployeeHello Song,
Yes, you are correct, this example is essentially replaced by this new model:
https://www.comsol.com/model/design-optimization-of-a-beam-71731
The workflow in 6.0 is substantially easier.