Micromirrors have two key benefits: low power consumption and low manufacturing costs. For this reason, many industries use micromirrors for a wide range of MEMS applications. To save time and money when designing micromirrors, engineers can accurately account for thermal and viscous damping and analyze device performance via the COMSOL Multiphysics® software.
The Many Applications of Micromirrors
Picture a micromirror as a single string on a guitar. The string is so light and thin that when you pluck it, the surrounding air dampens the string’s motion, bringing it to a standstill.
Micromirrors have a wide variety of potential applications. For instance, these mirrors can be used to control optic elements, an ability that makes them useful in the microscopy and fiber optics fields. Micromirrors are found in scanners, heads-up displays, medical imaging, and more. Additionally, MEMS systems sometimes use integrated scanning micromirror systems for consumer and telecommunications applications.

Close-up view of an HDTV micromirror chip. Image by yellowcloud — Own work. Licensed under CC BY 2.0, via Flickr Creative Commons.
When developing a micromirror actuator system, engineers need to account for its dynamic vibrating behavior and damping, both of which greatly affect the operation of the device. Simulation provides a way to analyze these factors and accurately predict system performance in a timely and cost-efficient manner.
To perform an advanced MEMS analysis, you can combine features in the Structural Mechanics Module and Acoustics Module, two add-on products to the COMSOL Multiphysics simulation platform. Let’s take a look at frequency-domain (time-harmonic) and transient analyses of a vibrating micromirror.
Performing a Frequency-Domain Analysis of a Vibrating Micromirror
We model an idealized system that consists of a vibrating silicon micromirror — which is 0.5 by 0.5 mm with a thickness of 1 μm — surrounded by air. A key parameter in this model is the penetration depth; i.e., the thickness of the viscous and thermal boundary layers. In these layers, energy dissipates via viscous drag and thermal conduction. The thickness of the viscous and thermal layers is characterized by the following penetration depth scales:
where f is the frequency, \rho is the fluid density, \mu is the dynamic viscosity, \kappa is the coefficient of thermal conduction, C_\textrm{p} is the heat capacity at constant pressure, and \textrm{Pr} is the nondimensional Prandtl number.
For air, when the system is excited at a frequency of 10 kHz (which is typical for this model), the viscous and thermal scales are 22 µm and 18 µm, respectively. These are comparable to the geometric scales, like the mirror thickness, meaning that thermal and viscous losses must be included. Moreover, in real systems, the mirrors may be located near surfaces or in close proximity to each other, creating narrow regions where the damping effects are accentuated.
The frequency-domain analysis provides insight into the frequency response of the system, including the location of the resonance frequencies, Q factor of the resonance, and damping of the system.
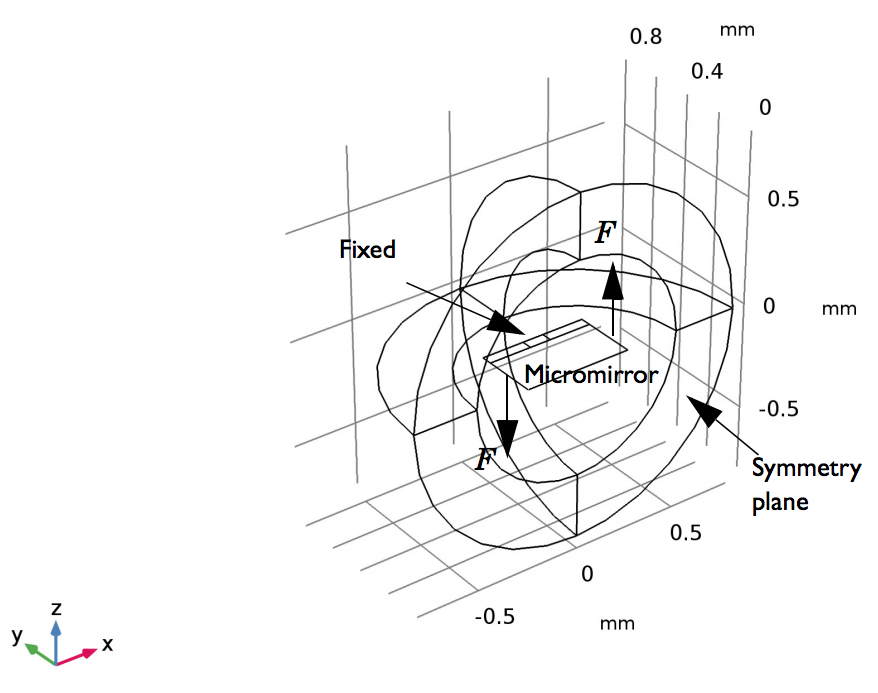
The micromirror model geometry, showing the symmetry plane, fixed constraint, and torquing force components.
In this example, we use three separate interfaces:
- The Shell interface to model the solid micromirror, available in the Structural Mechanics Module
- The Thermoviscous Acoustics, Frequency Domain interface to model the air domain around the mirror, available in the Acoustics Module
- The Pressure Acoustics, Frequency Domain interface to truncate the computational domain, available in the Acoustics Module
By modeling the detailed thermoviscous acoustics and using the Thermoviscous Acoustics, Frequency Domain interface, we can explicitly include thermal and viscous damping while solving the full linearized Navier-Stokes, continuity, and energy equations. In doing so, we accomplish one of the main goals for this model: accurately calculating the damping experienced by the mirror.
To set up and combine the three interfaces, we use the Acoustics-Thermoviscous Acoustics Boundary and Thermoviscous-Acoustics-Structure Boundary multiphysics couplings. We then solve the model using a frequency-domain sweep and an eigenfrequency study. These analyses enable us to study the resonance frequency of the mirror under a torquing load in the frequency domain.
Results of the Frequency-Domain Analysis
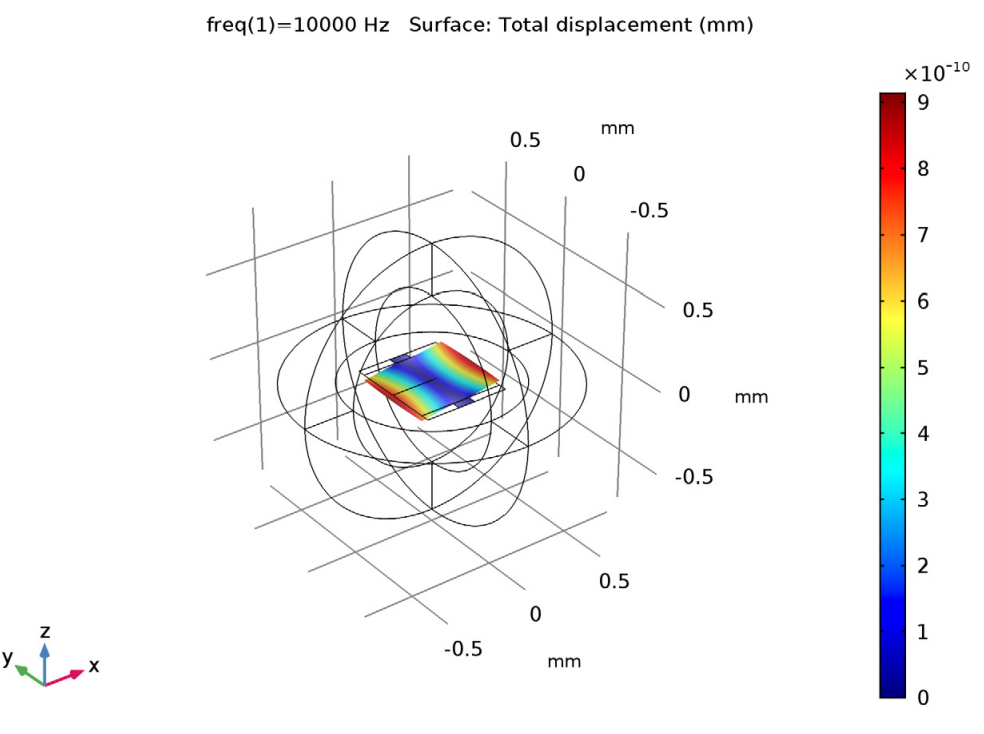
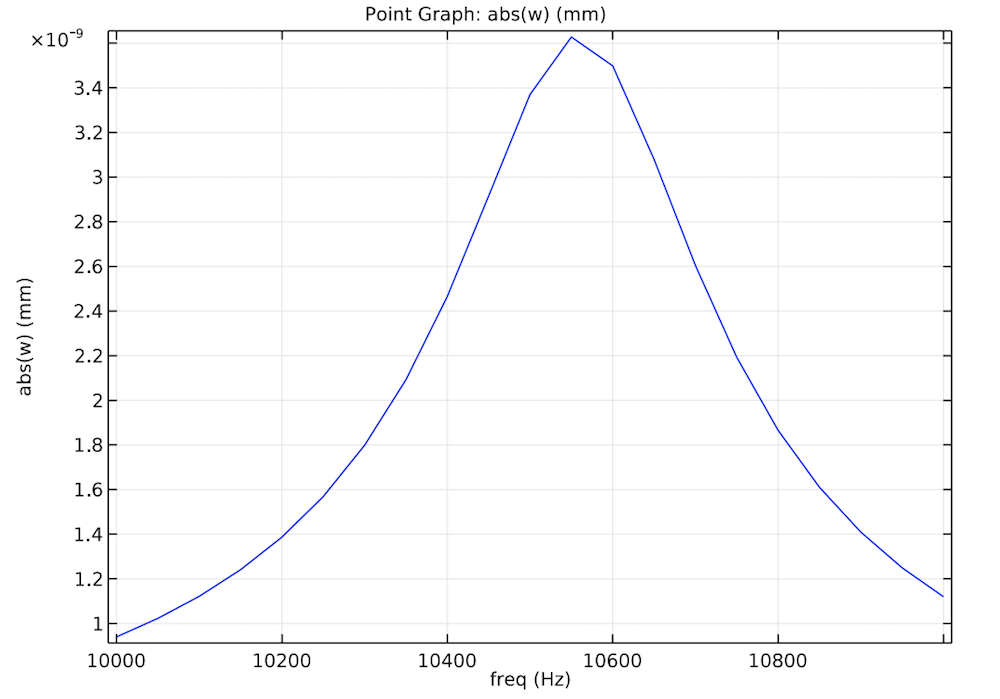
Let’s take a look at the displacement of the micromirror for a frequency of 10 kHz and when exposed to the torquing force. In this scenario, the displacement mainly occurs at the edges of the device. To view displacement in a different way, we also plot the response at the tip of the micromirror over a range of frequencies.
Micromirror displacement at 10 kHz for phase 0 (left) and the absolute value of the z-component of the displacement field at the micromirror tip (right).
Next, let’s view the acoustic temperature variations (left image below) and acoustic pressure distribution (right image below) in the micromirror for a frequency of 11 kHz. As we can see, the maximum and minimum temperature fluctuations occur opposite to one another and there is an antisymmetric pressure distribution. The temperature fluctuations are closely related to the pressure fluctuations through the equation of state. Note that the temperature fluctuations fall to zero at the surface of the mirror, where an isothermal condition is applied. The temperature gradient near the surface gives rise to the thermal losses.
Temperature fluctuation field within the thermoviscous acoustics domain (left) and the pressure isosurfaces (right).
The two animations below show a dynamic extension of the frequency-domain data using the time-harmonic nature of the solution. Both animations depict the mirror movement in a highly exaggerated manner, with the first one showing an instantaneous velocity magnitude in a cross section and the second showing the acoustic temperature fluctuations. These results indicate that there are high-velocity regions close to the edge of the micromirror. We determine the extent of this region into the air via the scale of the viscous boundary layer (viscous penetration depth). We can also identify the thermal boundary layer or penetration depth using the same method.
Animation of the time-harmonic variation in the local velocity.
Animation of the time-harmonic variation in the acoustic temperature fluctuations.
When the problem is formulated in the frequency domain, eigenmodes or eigenfrequencies can also be identified. From the eigenfrequency study (also performed in the model), we can determine the vibrating modes, shown in the animation below (only half the mirror is shown as symmetry applies). Our results show that the fundamental mode is around 10.5 kHz, with higher modes at 13.1 kHz and 39.5 kHz. The complex value of the eigenfrequency is related to the Q factor of the resonance and thus the damping. (This relationship is discussed in detail in the Vibrating Micromirror model documentation.)
Animation of the first three vibrating modes of the micromirror.
Transient Analysis of Viscous and Thermal Damping in a Micromirror
As of version 5.3a of the COMSOL® software, a different take on this example solves for the transient behavior of the micromirror. Using the same geometry, we extend the frequency-domain analysis into a transient analysis. To achieve this, we swap the frequency-domain interfaces with their corresponding transient interfaces and adjust the settings of the transient solver. In the simulation, the micromirror is actuated for a short time and exhibits damped vibrations.
The resulting model includes some of the most advanced air and gas damping mechanisms that COMSOL Multiphysics has to offer. For instance, the Thermoviscous Acoustics, Transient interface generates the full details for the viscous and thermal damping of the micromirror from the surrounding air.
In addition, by coupling the transient perfectly matched layer capabilities of pressure acoustics to the thermoviscous acoustics domain, we can create efficient nonreflecting boundary conditions (NRBCs) for this model in the time domain.
Results of the Transient Analysis
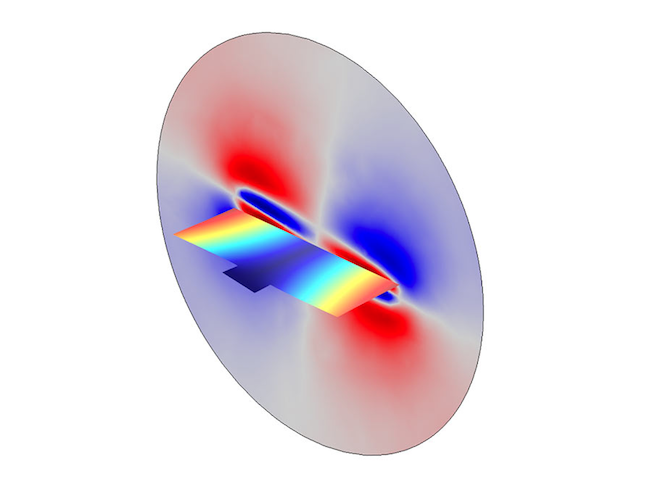
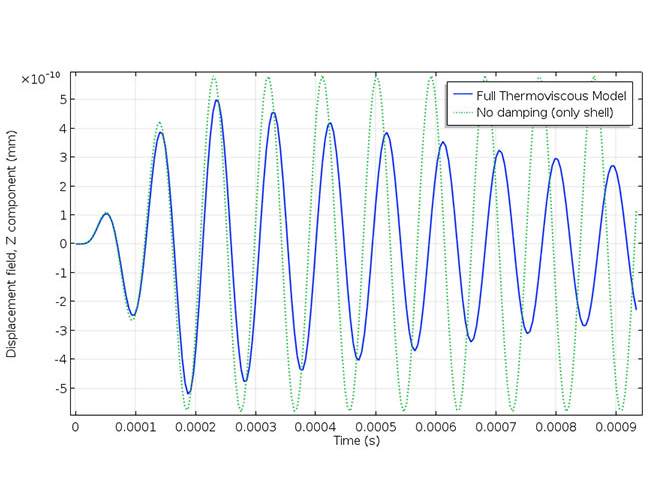
Let’s start with the displacement results. The 3D results (left image below) visualize the displacement of the micromirror and the pressure distribution at a given time. We also generate a plot (right image below) to illustrate the damped vibrations caused by thermal and viscous losses. The green curve represents the undamped response of the micromirror when the surrounding air is not coupled to the mirror movement. The time-domain simulations make it possible to study transients of the system, like the decay time, and the response of the system to an anharmonic forcing.
Micromirror displacement and pressure distribution (left) and the transient evolution of the mirror displacement (right).
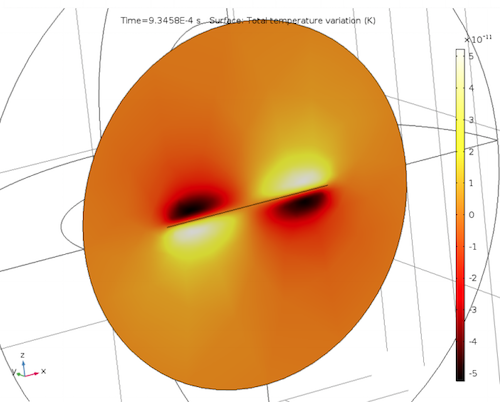
We can also examine the acoustic temperature variations surrounding the micromirror. The isothermal condition at the micromirror surface produces an acoustic thermal boundary layer. As with the frequency-domain example, the highest and lowest temperatures are located opposite to one another.
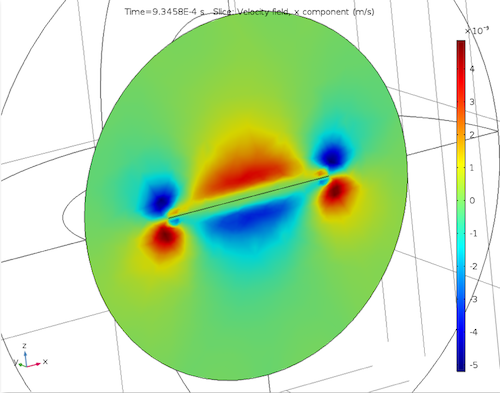
In addition, by calculating the acoustic velocity variations of the micromirror, we see that a no-slip condition at the micromirror surface results in a viscous boundary layer.
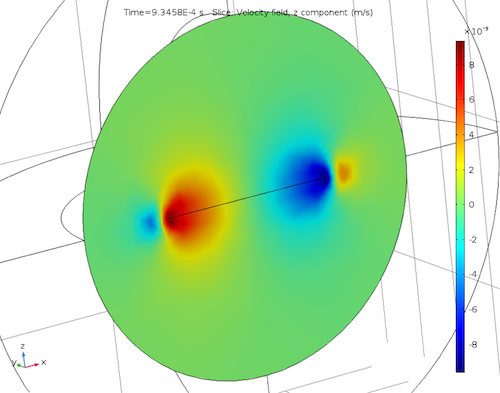
Acoustic temperature variations (left) as well as acoustic velocity variations for the x-component (center) and z-component (right).
Next Steps
These examples demonstrate that we can analyze micromirrors using advanced modeling features available in the Acoustics Module in combination with the Structural Mechanics Module. For more details on modeling micromirrors, check out the tutorials below.








Comments (1)
mona aghaee
January 29, 2018Hi,
I have problem modeling radiation heat transfer in a slab. A constant radiation hits an slab and part of that id transferred through the slab, part is absorbed within the slab and part is reflected. How should I model this? There are a lot of complicated models answered but none of them works for this. where and how could i enter transmisivity and reflectivity of the slab? Could you please give some information?
Thanks
Mona